1、计算题  一辆巡逻车最快能在10 s内由静止匀加速到最大速度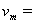50 m/s，并能保持这个速度匀速行驶，问该巡逻车在平直的高速公路上由静止追上前方2000 m处正以v=35 m/s的速度匀速行驶的汽车，至少需要多少时间？

参考答案：解：设至少经过时间t追上，则
? ?
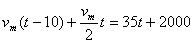? 代入数据解得 t=150s

本题解析：

本题难度：一般

2、填空题  一个做匀加速直线运动的物体，在连续的两个5 s内通过的位移分别为30 m和80 m，则这个物体的初速度和加速度分别为        m/s和         m/s2。

参考答案：1，2。

本题解析：分析：据题，物体做匀加速直线运动，在连续两个5s的时间间隔内所通过的位移分别为30m和80m，根据推论△x=aT2求出加速度，再由位移公式求出这个物体的初速度．
解答：解：由题，物体做匀加速直线运动，T=5s，x1=30m，x2=80m
根据推论△x=aT2得，x2-x1=aT2，得到 a=m/s2=2m/s2
又x1=v0T+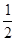aT2，得到v0=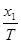-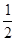aT，代入解得，v0=1m/s
故答案为：1m/s，2/s2
点评：本题运用匀变速直线运动的推论求解的，也可以运用运动学的位移公式分别对两段位移进行列式，得到关于加速度和初速度的两个方程，再解方程组．

本题难度：一般

3、计算题  （12分）体育老师带领学生做了一个游戏，在跑道上距离出发点50m的直线上放有1枚硬币，游戏规则是学生从出发点起跑把这枚硬币捡起来（捡硬币时，人的速度为0），看谁用的时间最短。已知某同学做加速运动和减速运动的加速度最大值均为a="2" m/s 2，运动的最大速度v不超过8 m/s。求该同学从出发点起跑到捡起这枚硬币所需要的最短时间。

参考答案：10.25s

本题解析：由题意分析，该同学在运动过程中，平均速度越大时间最短。可能先加速，再减速。也可能先加速，再匀速最后减速。
设先加速到8m/s再减速到零时位移为x，则加速时间t= v/a=4s                        （2分）
在2t时间内的位移为：x=.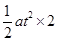.==32m                       （2分）
因为x=32m＜50 m，故该同学必然经历先加速，再匀速，最后减速的运动过程。        （2分）
该同学匀速运动的位移为：x′=50 m

本题难度：一般

4、选择题  一物体在A、B两点的正中间由静止开始运动（设不会超越A、B），其加速度随时间变化如图所示。设向A的加速度为为正方向，若从出发开始计时，则物体的运动情况是（?）

A 先向A ，后向B，再向A，又向B，4秒末静止在原处
B 先向A ，后向B，再向A，又向B，4秒末静止在偏向A的某点
C 先向A ，后向B，再向A，又向B，4秒末静止在偏向B的某点
D 一直向A运动，4秒末静止在偏向A的某点

参考答案：D

本题解析：根据a-t图象作出其v-t图象，如右图所示，
由该图可以看出物体的速度时大时小，但方向始终不变，
一直向A运动，又因v-t图象与t轴所围“面积”数值上
等于物体在t时间内的位移大小，所以4秒末物体距A点为
2米

本题难度：一般

5、计算题  据报道，一儿童玩耍时不慎从45m高的阳台上无初速度掉下，在他刚掉下时恰被楼下一社区管理人员发 现，该人员迅速由静止冲向儿童下落处的正下方楼底，准备接住儿童，已知管理人员到楼底的距离为18m，为确保能稳妥安全接住儿童，管理人员将尽力节约时间，但又必须保证接住儿童时没有水平方向的 冲击，不计空气阻力，将儿童和管理人员都看作质点，设管理人员奔跑过程中只做匀速或匀变速运动， g取10m/s2。
(1)管理人员至少用多大的平均速度跑到楼底？
(2)若管理人员在奔跑过程中做匀加速或匀减速运动的加速度大小相等，且最大速度不超过9m/s，求管理人员奔跑时加速度的大小需满足什么条件？

参考答案：解：(1)儿童下落过程，由运动学公式得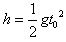?①
管理人员奔跑的时间t≤t0 ②
对管理人员奔跑过程，由运动学公式得s=t ③
由①②③并代入数据得≥6m/s
(2)假设管理人员先匀加速接着匀减速奔跑到楼底，奔跑过程中的最大速度为v0
由运动学公式得，得v0=2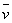= 12m/s>vm=9m/s
故管理人员应先加速到vm=9m/s，再匀速，最后匀减速奔跑到楼底
设匀加速、匀速、匀减速过程的时间分别为t1、t2、t3，位移分别为x1、x2、x3
由运动学公式得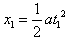?④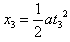，?⑤，x2=vmt2 ⑥，vm=at1=at3 ⑦，t1+t2+t3≤t0 ⑧，x1+x2+x3=s⑨
由④～⑨并代入数据得a≥9m/s2

本题解析：

本题难度：一般