1、选择题 一物体以5m/s的初速度，-2m/s2的加速度在粗糙水平面上滑行，在3s内物体通过的位移大小为
A.4?m
B.6.25?m
C.36?m
D.0
参考答案：B
本题解析：分析：根据匀变速直线运动的速度时间公式先求出物体在水平面上速度减为零的时间，因为物体速度为零后不再运动，再根据位移时间公式求出位移的大小．
解答：物体速度减为零所需的时间t0=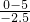
s=2.5s＜3s；
故3s内物体通过的位移大小为：x=v0t0+
at02=5×2.5-×2×2.52m=6.25m；
故选B．
点评：本题属于运动学中的刹车问题，是道易错题，求解位移时必须先求出速度减小为零所需的时间，因为速度为零后物体不再运动．
本题难度：困难
2、计算题 一辆客车在某高速公路上行驶，在经过某直线路段时，司机驾车做匀速直线运动。司机发现其正要通过正前方高山悬崖下的隧道，于是鸣笛，5s后听到回声；听到回声后又行驶10s司机第二次鸣笛，3s后听到回声。请根据以上数据帮助司机计算一下客车的速度，看客车是否超速行驶，以便提醒司机安全行驶。已知此高速公路的最高限速为110km/h（如图所示），声音在空中的传播速度为340m/s。
参考答案：解：设客车行驶速度为v1，声速为v2，客车第一次鸣笛时客车离悬崖的距离为L。由题意可知：
在第一次鸣笛到听到回声的过程中，应有2L－v1×5＝v2×5
当客车第二次鸣笛时，客车距离悬崖的距离为L′＝L－v1×15
同理有2L′－v1×3＝v2×3
即2(L－v1×15)－v1×3＝v2×3
得v1＝
＝24.3m/s＝87.5km/h，小于110km/h，故客车未超速
本题解析：
本题难度：困难
3、计算题 一辆汽车，以36km/h的速度匀速行驶10s，然后以1m/s2的加速度匀加速行驶10s，求：
（1）汽车在这20s内的位移是多大？
（2）汽车在加速的10s内的平均速度是多大？
参考答案：（1）
（2）
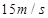
本题解析：已知
，
，
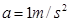（1）匀速行驶10s内位移：
匀加速行驶的10s内位移：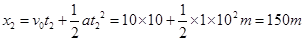
汽车在20s内的位移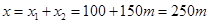
（2）根据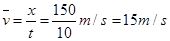
考点：考查了匀变速直线运动规律的应用
本题难度：一般
4、选择题 如图所示，长为s的光滑水平面左端为竖直墙壁，右端与半径为R光滑圆弧轨道相切于B点．一质量为m的小球从圆弧轨道上离水平面高为h（h?R）的A点由静止下滑，运动到C点与墙壁发生碰撞，碰撞过程无机械能损失，最终小球又返回A点；之后这一过程循环往复地进行下去，则小球运动的周期为（ ）
A．π
+s
B．2π+s
C．π+s
D．2π+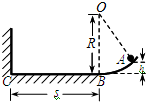
参考答案：A
本题解析：
本题难度：一般
5、选择题 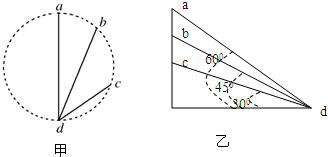 如图甲中ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点．图乙中ad、bd、cd是竖直面内三根倾角分别为60°、45°、30°的光滑细杆．每根杆上都套着一个小滑环（图中未画出），滑环分别从顶端a、b、c处释放（初速度为0），比较滑环由顶端下滑到底端的时间t，则
A.甲图中沿ad杆下滑的时间最短
B.甲图中沿ad、bd、cd杆的下滑的时间相同
C.乙图中沿bd杆下滑的时间最短
D.乙图中沿ad、bd、cd杆的下滑的时间相同
参考答案：BC
本题解析：分析：先受力分析后根据牛顿第二定律计算出滑环沿任意一根杆滑动的加速度，然后根据位移时间关系公式计算出时间，对表达式分析，得出时间与各因素的关系后得出结论．
解答：对于甲图，对小滑环，受重力和支持力，将重力沿杆的方向和垂直杆的方向正交分解，根据牛顿第二定律得小滑环做初速为零的匀加速直线运动的加速度为：a=gsinθ（θ为杆与水平方向的夹角）
由图中的直角三角形可知，小滑环的位移S=2Rsinθ
由S= ，得：t= = =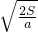
所以，t与θ无关，即t1=t2=t3．故A错误，B正确．
对于乙图，设斜面的底边长为L，倾角为α时，物体的加速度为a=gsinα
由  ==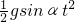
得 t=
根据数学知识得知，当α=45°时，t最小，即沿bd杆下滑的时间最短，故C正确，D错误．
故选BC
点评：本题关键从众多的杆中抽象出一根杆，假设其与水平方向的夹角为θ，然后根据牛顿第二定律求出加速度，再根据运动学公式求出时间表达式讨论．
本题难度：困难
|
|
|
问题咨询请搜索关注"91考试网"微信公众号后留言咨询
|
|
|
|
考试问吧
