1、简答题  质量为20kg的物体与水平面间的动摩擦因数为0.2，用一水平面成37°角，大小为100N的斜向上的拉力，使物体由静止开始运动，10S后再撤去拉力，g=10m/s2．求：（1）物体运动的加速度；（2）拉力F做的功．

参考答案：（1）物体的受力情况如图，根据牛顿第二定律得
? Fcos37°-f=ma
? N+Fsin37°=mg
又f=μN
联立得Fcos37°-μ（mg-Fsin37°）=ma
代入解得a=2.6m/s2
（2）10s内物体的位移为x=12at2=130m
拉力F做的功为W=Fxcos37°=100×130×0.8J=10400J
答：
（1）物体运动的加速度为2.6m/s2；
（2）拉力F做的功为10400J．

本题解析：

本题难度：一般

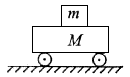
2、计算题  如图所示，小车质量M为2.0kg，它与水平地面摩擦力忽略不计，物体质量m为0.5kg，物体与小车间的动摩擦因数为0.3。求：
（1）小车在外力作用下以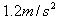的加速度向右运动时，物体受摩擦力多大？
（2）欲使小车产生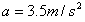的加速度，需给小车提供多大的水平推力？
（3）若要使物体m脱离小车，则至少用多大的水平力推小车？
（4）若小车长L＝1m，静止小车在8.5N水平推力的作用下，物体由车的右端向左滑动，则滑离小车需多长时间？（物体m看作质点）

参考答案：解：先求两者相对静止时的最大加速度，由牛顿第二定律知
（1）当时，物体与小车相对静止，静摩擦力产生了加速度
由牛顿第二定律得
?
（2）当时，物体与小车发生了相对滑动，物体对小车的摩擦力大小为

对小车，由牛顿第二定律得
所以，需给小车提供的推力为
（3）要使物块m脱离小车，则必须有
由牛顿第二定律得
解得
即至少用7.5N的力推小车
（4）由于F＝8.5N，大于水平推力7.5N，所以物体会滑落
对小车，由牛顿第二定律：
物体的加速度
物体m的位移①
小车的位移②
又因为③
联立①②③得运动时间

本题解析：

本题难度：困难

3、简答题  如图所示，质量为m的矩形线框MNPQ，MN边长为a，NP边长为b；MN边电阻为R1，PQ边电阻为R2，线框其余部分电阻不计．现将线框放在光滑绝缘的水平桌面上，PQ边与y轴重合．空间存在一个方向垂直桌面向下的磁场，该磁场的磁感应强度沿y轴方向均匀，沿x轴方向按规律Bx=B0（1-kx）变化，式中B0和k为已知常数且大于零．矩形线框以初速度v0从图示位置向x轴正方向平动．求：
（1）在图示位置时线框中的感应电动势以及感应电流的大小和方向；
（2）线框所受安培力的方向和安培力的表达式；
（3）线框的最大运动距离xm；
（4）若R1=2R2，线框运动到

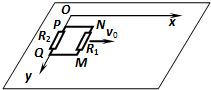
参考答案：（1）E=△Φ△t=ab△B△t=ab△B△x△x△T=kabv0B0
I=ER1+R2=kabv0B0R1+R2
感应电流方向沿：NPQMN
（2）线框受的安培力水平向左，安培力为：
F=aI△B=k2a2b2B20R1+R2v
（3）根据牛顿第二定律知：
F=F1-F2=m△v△t=-(kabB0)2△x(R1+R2)△t
其中m△v=-(kabB0)2△xR1+R2
mv0=(kabB0)2xmR1+R2
联立解得xm=mv0(R1+R2)(kabB0)2
（4）由m△v=-(kabB0)2△xR1+R2得：
m（v-v0）=-(kabB0)2xm2(R1+R2)=-12mv0，v=v02
Q=△EK=12mv20-12m(v2)2=38mv20
电阻R1产生的热为
QR1=R1R1+R2Q=14mv20
答：（1）在图示位置时线框中的感应电动势为kabv0B0
感应电流的大小为kabv0B0R1+R2，方向沿NPQMN；
（2）线框所受安培力的方向水平向左，安培力的表达式为k2a2b2B20R1+R2v；
（3）线框的最大运动距离mv0(R1+R2)(kabB0)2；
（4）线框运动到xm2过程中，电阻R1产生的焦耳热14mv20．

本题解析：

本题难度：一般

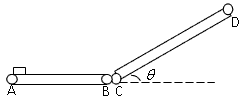
4、计算题  如图所示为仓库中常用的皮带传输装置示意图，它由两台皮带传送机组成，一台水平传送，A、B两端相距3m；另一台倾斜，传送带与地面的倾角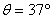，C、D两端相距4.45m，B、C相距很近。水平部分AB以5m/s的速率顺时针转动。将质量为10kg的米袋（可视为质点）放在A端，到达B端后，速度大小不变地传到倾斜部分，米袋与传送带间的动摩擦因数均为0.5。g取10m/s2。试求：
（1）若CD部分传送带不运转，米袋沿着CD传送带所能上升的最大距离；
（2）若要米袋能被送到D端，CD部分顺时针运转的速度应满足的条件及米袋从C端到D端所用时间的取值范围。

参考答案：解：（1）米袋在AB上加速时的加速度
? 米袋的速度达到时，滑行的距离，因此米袋在到达B点之前就有了与传送带相同的速度
? 设米袋在CD上运动的加速度大小为a，由牛顿第二定律得
? 代入数据得
? 所以能滑上的最大距离
（2）设CD部分运转速度为时，米袋恰能到达D点（即米袋到达D点时速度恰好为零）
? 则米袋速度减为之前的加速度为
? 米袋速度小于至减为零前的加速度为
? 由解得
? 即要把米袋送到D点，CD部分的速度
? 米袋恰能运到D点所用时间最长为
? 若CD部分传送带的速度较大，使米袋沿CD上滑时所受摩擦力一直沿皮带向上，则所用时间最短，此种情况米袋加速度一直为
? 由
? 所以，所求的时间t的范围为

本题解析：

本题难度：困难

5、选择题  平行板间加如图所示周期变化的电压，重力不计的带电粒子静止在平行板中央，从t=0时刻开始将其释放，运动过程无碰板情况．图中，能定性描述粒子运动的速度图象正确的是（　　）
A．

B．

C．

D．