1、选择题  如图所示，abcd为一正方形边界的匀强磁场区域，磁场边界边长为L，三个粒子以相同的速度从a点沿ac方向射入，粒子1从b点射出，粒子2从c点射出，粒子3从cd边垂直于磁场边界射出，不考虑粒子的重力和离子间的相互作用．根据以上信息，可以确定（　　）
A．粒子1带负电，粒子2不带电，粒子3带正电
B．粒子1和粒子3的比荷之比为2：1
C．粒子1和粒子2在磁场中运动时间之比为4：1
D．粒子3的射出位置与d点相距

参考答案：A、根据左手定则可得：粒子1带正电，粒子2不带电，粒子3带负电．故A错误；
B、做出粒子运动的轨迹如图，则粒子1运动的半径：r1=L

本题解析：

本题难度：一般

2、计算题  （22分）如图所示，空间存在两个匀强磁场，它们分界线是边长为3L的等边三角形APC，D、E、F三点分别在PC、CA、AP边上，AF =" PD" =" CE" = L，分界线两侧的磁场方向相反且垂直于纸面，磁感应强度大小相同，均为B，分界线外的磁场区域足够大。现有一质量为m、电荷量为q的带正电离子(不计重力)，从F点以速度v向三角形内射入。

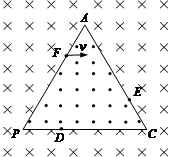
(1)如果速度v方向与PC边平行，离子第一次到分界线就经过D点，则磁感应强度B的大小是多少？
(2)如果改变磁感应强度B的大小和速度v的方向（速度v的方向均在纸平面内），使离子第一次、第二次到达分界线时依次经过D点和E点，求离子周期性运动的周期。
(3)再改变磁感应强度B的大小和速度v的方向（速度v的方向均在纸平面内），能否仍使离子第一次、第二次到达分界线时依次经过D点和E点？为什么？

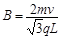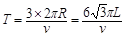参考答案：（1）（2）（3）不可能

本题解析：解: (22分)
(1) 带电离子的运动轨迹如图所示,

可得圆周运动的半径
? [2分]
根据洛仑兹力提供向心力，可得
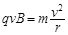? [1分]
由上二式可得?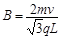?[2分]
（2）连接D、E、F，可得DDEF是等边三角形，当离子沿?DFE的角平线方向射入时, 离子才能依次经过D点、E点，其运动的各段轨迹依次是a、b、c、d、e、f.回到F点, 完成一个周期运动, 如右下图所示.

画出a段圆孤的圆心O，由几何关系可知，DFOD也是等边三角形，所以圆孤半径
R =" OF" =" FD" =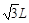? [3分]
离子一个周期运动的路径为3个圆的周长，所以其运动周期
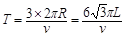? [8分]
(3) 不可能.? [2分]
右图中三个圆相切是满足题中要求的
必要条件, 再改变B的大小和v的方
向, 圆半径R将改变, 半径R无论变
大还是变小, 三圆总是相交, 不可能
再相切, 所以不可能. [4分]
本题考查的是对带电粒子在磁场中的运动问题，根据带电粒子在磁场中运动受的洛伦兹力的情况，粒子做圆周运动，利用几何关系，即可求解；

本题难度：一般

3、选择题  如图所示，在x轴上方存在垂直于纸面向里的匀强磁场，磁感应强度为B．在xOy平面内，从原点O处沿与x轴正方向成θ角（0＜θ＜π）以速率v发射一个带正电的粒子（重力不计）．则下列说法正确的是（　　）
A．若θ一定，v越大，则粒子在磁场中运动的时间越短
B．若θ一定，v越大，则粒子在磁场中运动的角速度越大
C．若v一定，θ越大，则粒子在磁场中运动的时间越短
D．若v一定，θ越大，则粒子在离开磁场的位置距O点越远