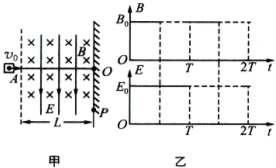
1、简答题  如图甲所示，真空区域内有一粒子源A，能每隔

参考答案：由于t=3T2时刻到达虚线的粒子在=2T时刻到达荧光屏上的O点，而在t=3T2～t=2T期间电场和磁场都为零，粒子沿直线运动到O点，说明粒子的重力不计，故：
（1）t=0时刻进入的粒子受到的电场力和洛伦兹力平衡，故做匀速直线运动，在t=T2时刻到达O点．
（2）t=T2时刻进入的粒子只受电场力作用，做类平抛运动，t=T时刻到达P点，OP=L2．
（3）t=T时刻进入的粒子只受洛伦兹力作用，则得
x=v0?T2=L
得Lv0=T2或v0T=2L
由y=12?E0qm?(T2)2=L2得
mE0q=T24L
又由qv0B=mv20R，联立得R=mv0qB=L
粒子在磁场中运动的周期为 T0=2πmqB=πT
设经过T2时间即3T2时刻粒子运动到F点，设此过程中粒子转过的圆心角为θ，则
θ2π=12TπT，则得θ=1rad
以后粒子不受力做匀速直线运动的打到Q点，由QO点间的距离为
yQO=（L-Lcosθ）+（L-Lsinθ）tanθ=（L-Lcos1）+）+（L-Lsin1）tan1；
（4）t=3T2时刻到达虚线位置的粒子做匀速直线运动在t=2T时刻到达荧光屏上的O点；
（5）以后重复，即：t=2kT（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+12）T（k=0，1，2，3，…）时刻到达O点；
t=（2k+12）T（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+1）T（k=0，1，2，3，…）时刻到达P点；
t=（2k+1）T（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+1）T+T2+L-sin1v0cos1（k=0，1，2，3，…）时刻到达Q点；
t=（2k+32）T（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+2）T（k=0，1，2，3，…）时刻到达O点．
答：
t=2kT（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+12）T（k=0，1，2，3，…）时刻到达O点；
t=（2k+12）T（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+1）T（k=0，1，2，3，…）时刻到达P点；
t=（2k+1）T（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+1）T+T2+L-sin1v0cos1（k=0，1，2，3，…）时刻到达Q点；
t=（2k+32）T（k=0，1，2，3，…）时刻到虚线位置的粒子，在t=（2k+2）T（k=0，1，2，3，…）时刻到达O点．

本题解析：

本题难度：一般

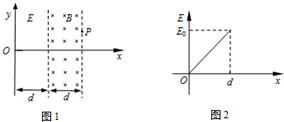
2、简答题  如图1所示，在x轴上0到d范围内存在电场（图中未画出），x轴上各点的电场沿着x轴正方向，并且电场强度大小E随x的分布如图2所示；在x轴上d到2d范围内存在垂直纸面向里的匀强磁场，磁感应强度大小为B．一质量为m，电量为+q粒子沿x轴正方向以一定速度从O点进入电场，最终粒子恰从坐标为（2d，

参考答案：（1）由图象，x=0.5d处，电场强度为E=0.5E0，由牛顿第二定律得：
qE=ma
解得：a=qE02m．
（2）在磁场中运动轨迹如图，设半径为R，由几何关系
R2=d2+(R-

本题解析：

本题难度：一般

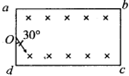
3、选择题  如图所示，一矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场（ab、dc边足够长），现从矩形区域ad边的中点O处，垂直磁场射入一速度方向与ad边夹角为30°、大小为v0的带正电粒子，已知粒子质量为m，电荷量为q，ad边长为l，重力影响不计，要使粒子从ab边上射出磁场，则（　　）
A．只要粒子的速度小于