1、实验题  一个质子和一个?α?粒子同时射入同一匀强磁场中，射入方向和磁场垂直，则：
如果两者以相同的速度进入磁场中，则其圆运动的轨道半径之比是_______；
如果两者以相同的动量进入磁场中，则其圆运动的轨道半径之比是_______；
如果两者以相同的动能进入磁场中，则其圆运动的轨道半径之比是_______.

参考答案：1∶2　2∶1　1∶1

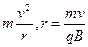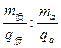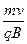本题解析：因为qvB＝m，所以当速度相同时，r质∶rα＝＝1∶2；当动量相同时，r质∶rα＝＝2∶1；当动能相等时，qvB＝m，得r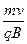＝，又由Ek?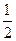＝mv2，可得：r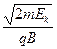＝，r质∶rα＝.

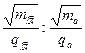本题难度：一般

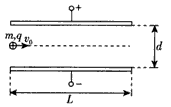
2、计算题  如图所示，两块相同的金属板正对着水平放置，金属板长为L，两板间距离为d，上极板的电势比下极板高U。质量为m、带电量为q的正离子束，沿着两板间中心轴线，以初速度v0进入两板间，最终都能从两板间射出。不计离子重力及离子间相互作用的影响。
(1)求离子在穿过两板的过程中沿垂直金属板方向上移动的距离y；
(2)若在两板间加垂直纸面的匀强磁场，发现离子束恰好沿直线穿过两板，求磁场磁感应强度B的大小和方向；
(3)若增大两板间匀强磁场的强度，发现离子束在穿过两板的过程中沿垂直金属板方向上移动的距离也为y，求离子穿出两板时速度的大小v。

参考答案：解：(1)离子在穿过两板的过程中，只受与初速度v0垂直的电场力F作用，且F=qE
两板间电场强度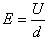
离子的加速度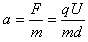
离子沿中心轴线方向做匀速直线运动，设离子穿过两板经历的时间为t，则L=v0t
离子沿垂直金属板方向上做初速度为0的匀变速直线运动，则
解得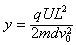
(2)离子束恰好沿直线穿过两板，说明离子受力平衡，即qE=qv0B
所以磁感应强度的大小，磁场的方向垂直纸面向里
(3)增大磁场的强度时，离子受洛伦兹力增大，所以离子会向上偏在离子穿过极板的过程中，电场力做负功，根据动能定理得
解得离子穿出两板时的速度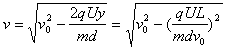

本题解析：

本题难度：困难

3、计算题  如图所示，匀强电场方向竖直向上，匀强磁场方向水平且垂直纸面向里，有两个带电小球a和b，a恰能在垂直于磁场方向的竖直平面内做半径r=0.8?m的匀速圆周运动，b恰能以v=2?m/s的水平速度在垂直于磁场方向的竖直平面内向右做匀速直线运动．小球a、b质量ma=10?g，mb=40?g，电荷量qa=1×10－2C，qb= 2×10－2C，g=10m/s2。求：
（1）小球a和b分别带什么电？电场强度E与磁感应强度B的大小？
（2）小球a做匀速周周运动绕行方向是顺时针还是逆时针？速度大小va是多大？
（3）设小球b的运动轨迹与小球a的运动轨迹的最低点相切，当小球a运动到最低点即切点时小球b也同时运动到切点，a、b相碰后合为一体，设为c，在相碰结束的瞬间，c的加速度ac=？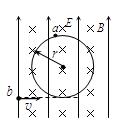

参考答案：（1）小球a在互相垂直的匀强电场和匀强磁场中做匀速圆周运动，电场力和重力的合力为零，电场力方向向上，所以小球a带正电，且有
mag=qaE··································································①
E="10?N" / C································································②
小球b做匀速直线运动，合力为零，带正电，且有
mbg=qbvB+qbE·····························································③
B=5T························ ·············································④
（2）小球a做匀速圆周运动绕行方向是逆时针方向。
由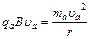
得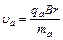······························································⑤
va="4?m" / s·································································⑥
（3）a、b相碰前速度方向相同，设碰后的共同速度为vc，则
ma va+mb v=(ma+mb) vc······················································⑦
vc="2.4?m" / s································································⑧
由牛顿第二定律得
mcac=qcE+qc vcB – meg······················································⑨
mc=ma+mb
qc=(qa+qb)
解得ac="3.2?m" / s2··························································⑩
评分标准：本题满分18分。其中判断a、b带电性质各1分，a绕行方向1分，①式2分，②式1分，③式2分，④式1分，⑤式2分，⑥式1分，⑦式2分，⑧式1分，⑨式2分，⑩式1分。

本题解析：略

本题难度：一般

4、计算题  两块足够大的平行金属极板水平放置，极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律分别如图甲、乙所示(规定垂直纸面向里为磁感应强度的正方向)。在t=0时刻由负极板释放一个初速度为零的带负电的粒子(不计重力)。若电场强度E0、磁感应强度B0、粒子的比荷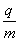均已知，且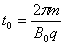，两板间距h=。
(1)求粒子在0～t0时间内的位移大小与极板间距h的比值。
(2)求粒子在极板间做圆周运动的最小半径R1与最大半径R2(用h表示)。
(3)若板间电场强度E随时间的变化仍如图甲所示，磁场的变化改为如图丙所示，试画出粒子在板间运动的轨迹图(不必写计算过程)。

参考答案：解：（1）粒子在0～t0时间内：S1=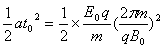
所以
（2）粒子在t0～2t0时间内做匀速圆周运动，运动速度v1=at0=
圆半径R1=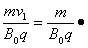
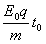
所以R1=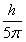
T=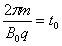，所以粒子在t0～2t0时间内恰好完成一个完整的圆周运动，粒子在2t0～3t0时间内做初速度为v1=at0=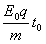的匀加速直线运动


粒子在3t0～4t0时间内，R2=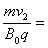2R1
由于s1+s2+R2+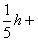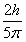＜h，所以粒子在3t0～4t0时间内继续做一个完整的匀速圆周运动，在4t0～5t0时间内做匀加速直线运动出去
所以，粒子做圆运动的最大半径为R2=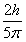
粒子在板间运动的轨迹图如图甲所示
（3）粒子在板间运动的轨迹图如图乙所示
?

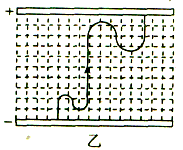
本题解析：

本题难度：困难

5、计算题  （14分）、传送带和水平面的夹角为37°，完全相同的两轮和皮带的切点A、B间的距离为24m， B点右侧（B点在场的边缘）有一上下无限宽左右边距为d的正交匀强电场和匀强磁场，电场方向竖直向上，匀强磁场垂直于纸面向里，磁感应强度B=103T.传送带在电机带动下，以4m/s速度顺时针匀速运转，现将质量为m=0.1kg，电量q=+10-2C的物体(可视为质点)轻放于传送带的A点，已知物体和传送带间的摩擦系数为μ=0.8，物体在运动过程中电量不变，重力加速度取g=10m/s2，sin37°=0.6，cos37°=0.8.求：

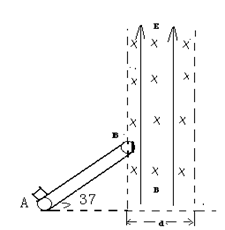
（1）物体从A点传送到B点的时间？
（2）若物体从B点进入混合场后做匀速圆周运动，则所加的电场强度的大小E应为多少？物体仍然从混合场的左边界出混合场，则场的右边界距B点的水平距离d至少等于多少？

参考答案：11s?0.016m

本题解析：物体在斜面上做加速运动，由牛顿第二定律有
μmgcos370-mgsin37°=ma
得a=μmgcos37°-gsin37°?（1分）
a=0.4m/s2?（1分）
物体做匀加速运动到与传送带有相同速度，有v=at1
t1=10s?（1分）
物体运动位移为x=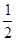at2?（1分）
得x=20m?（1分）
物体继续与传送带以相同速度匀速运动，有
LAB-X=vt2?（1分）
所以t2=1s?（1分）
物体在传送带上运动总时间t=t1+t2=11s?（1分）
物体在混合场中做匀速圆周运动，有gE=mg?（1分）
得E=100N/C?（1分）
qvB=m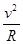? 1分? R=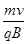=0.04m（1分）
物体离开混合场有sin370=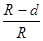?（1分）
d=0.016m? (1 分)

本题难度：一般