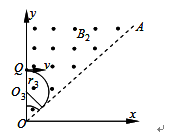
1、计算题  如图所示，在平行板电容器的两板之间，存在相互垂直的匀强磁场和匀强电场，磁感应强度B1=0.40T，方向垂直纸面向里，电场强度E=2.0×105V/m，PQ为板间中线．紧靠平行板右侧边缘xOy坐标系的第一象限内，有垂直纸面向外的匀强磁场，磁感应强度B2=0.25T，磁场边界AO和y轴的夹角∠AOy=45°．一束带电量q=8.0×10-19C的同位素正离子从P点射入平行板间，沿中线PQ做直线运动，穿出平行板后从y轴上坐标为（0，0.2m）的Q点垂直y轴射入磁场区，离子通过x轴时的速度方向与x轴正方向夹角在45°~90°之间，不计离子重力，求：

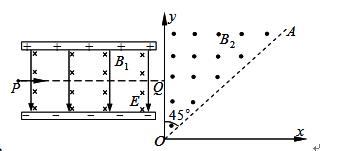
（1）离子运动的速度为多大？
（2）x轴上被离子打中的区间范围？
（3）离子从Q运动到x轴的最长时间？
（4）若只改变AOy区域内磁场的磁感应强度大小，使离子都不能打到x轴上，磁感应强度大小B2?应满足什么条件？

参考答案：
（1）5.0×105m/s（2）0.1m≤x≤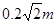（3）（4）B2?≥0.60T

本题解析：在有界磁场中带电粒子的运动经常涉及到临界问题，本题中带电粒子刚好穿出的临界条件就是与磁场边界相切，计算过程中的思路是先找圆心，后求半径
（1）：离子在两板间时有：?解得：v=5.0×105m/s?
（2）当通过x轴时的速度方向与x轴正方向夹角为45°时，
到达x轴上的M点，如图所示，则：
r1=0.2m?所以：OM= ?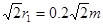
当通过x轴时的速度方向与x轴正方向夹角为90°时，
到达x轴上的N点，则：
r2=0.1m?所以：ON=r2=0.1m?
所以离子到达x轴的区间范围是0.1m≤x≤?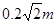
（3）所有离子速度都相同，当离子运动路程最长时，时间也最长，由图知当r=r1时离子运动时间最长，则：tm=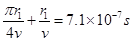
（4）由牛顿第二定律有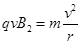： ?则：?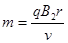
当r=r1时，同位素离子质量最大：?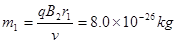
若质量最大的离子不能穿过直线OA，则所有离子必都不能到达x轴，由图可知使离子不能打到x轴上的最大半径：?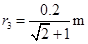
设使离子都不能打到x轴上，最小的磁感应强度大小为B0，则?
?
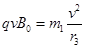解得? B0==0.60T?则：B2?≥0.60T?

本题难度：一般

2、计算题  如图（a）所示，两水平放置的平行金属板E、F相距很近，上面分别开有小孔O"、O，水平放置的平行金属导轨与E、F接触良好，且导轨在磁感强度为B1=10 T的匀强磁场中，导轨间距L=0.50 m，金属棒MN紧贴着导轨沿平行导轨方向在磁场中做往复运动，其速度图像如图（b）所示。若规定向右运动的速度方向为正方向，从t=0时刻开始，从F板小孔O处连续不断地以垂直于F板方向飘入质量为m=3.2×10-21 kg、电荷量q=1.6×10-19 C的 带正电的粒子（设飘入速度很小，可视为零）。在E板外侧有一矩形匀强磁场B2=10T，粒子经加速后从AB边中点与AB成30°夹角垂直进入磁场，AB相距d=10 cm，AD边足够长，B1、B2方向如图（a）所示，求：（粒子重力及其相互作用不计，计算结果保留两位有效数字）
（1）在0-4.0 s时间内哪些时刻发射的粒子能从磁场边界AD边飞出？
（2）粒子从磁场边界AD边射出来的范围为多少？

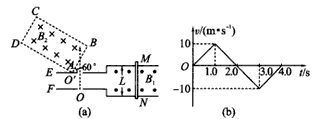
参考答案：解：（1）要从AD边飞出，临界两条轨迹如图所示，相应的圆心分别是O1、O2，由几何关系可得，大圆半径r1

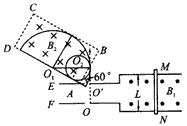
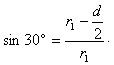，r1=d
小圆半径为r2，r2+r2sin30°=，，于是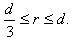
粒子在磁场中做圆周运动，洛伦兹力提供向心力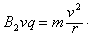
则v1=50 m/s，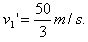
粒子在两板间加速，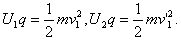
MN切割磁感线U1=B1L1v2，v2=5m/s，U2=B1L1v2"
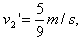由v-t图像可知a=10 m/s2，v2=at2，t2=0.5 s，v2"=at1，
由于棒的方向必须向右
由v-t图可得时间范围是0.056-0.5 s和1.5~1.944s
（2）由临界轨迹和几何关系可知，粒子从磁场边界AD射出的范围长度是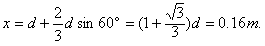

本题解析：

本题难度：困难

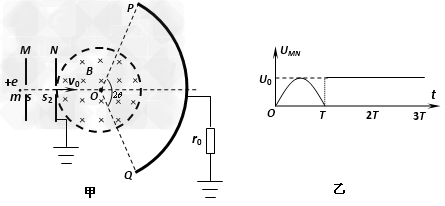
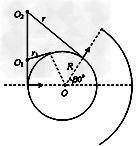
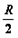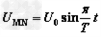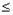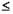3、计算题  如图甲所示，M、N为竖直放置的两块平行金属板，圆形虚线为与N相连且接地的圆形金属网罩（不计电阻）。PQ为与圆形网罩同心的金属收集屏，通过阻值为r0的电阻与大地相连。小孔s1、s2、圆心O与PQ中点位于同一水平线上。圆心角2θ=120°、半径为R的网罩内有大小为B，方向垂直纸面向里的匀强磁场。M、N间相距且接有如图乙所示的随时间t变化的电压，（0tT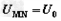），（t >T）（式中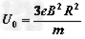，T已知），质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场，接着通过s2进入磁场。（质子通过M、N的过程中，板间电场可视为恒定，质子在s1处的速度可视为零，质子的重力及质子间相互作用均不计。）
（1）若质子在t >T时刻进入s1，为使质子能打到收集屏的中心需在圆形磁场区域加上一个匀强电场，求所加匀强电场的大小和方向？
（2）质子在哪些时间段内自s1处进入板间，穿出磁场后均能打到收集屏PQ上？
（3）若毎秒钟进入s1的质子数为n，则收集屏PQ电势稳定后的发热功率为多少？

参考答案：解：（1）在电场中，由动能定理得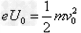
为使质子做匀速直线运动，有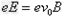
解得E=，方向竖直向下
（2）质子在板间运动，根据动能定理，有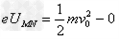
质子在磁场中运动，根据牛顿第二定律，有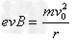
若质子能打在收集屏上，轨道半径r与半径R应满足的关系：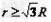
解得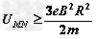

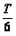
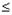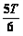结合图象可知：质子在t和t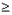T之间任一时刻从s1处进入电场，均能打到收集屏上
（3）稳定时，收集屏上电荷不再增加，即在t>T 时刻以后，此时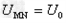，收集屏与地面电势差恒为U，U=Ir0?
单位时间到达收集板的质子数n
单位时间内，质子的总能量为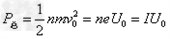
单位时间内屏上发热功率为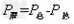
消耗在电阻上的功率为
所以收集板发热功率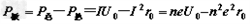

本题解析：

本题难度：困难

4、选择题  如图所示, 一块长度为a、宽度为b、厚度为d的金属导体, 当加有与侧面垂直的匀强磁场B, 且通以图示方向的电流I时, 用电压表测得导体上、下表面M、N间电压为U. 已知自由电子的电荷量为e. 下列说法中正确的是(　　)

A．M板比N板电势高
B．导体单位体积内自由电子数越多, 电压表的示数越大
C．导体中自由电子定向移动的速度为v=U/Bd
D．导体单位体积内的自由电子数为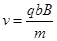

参考答案：CD

本题解析：自由电子为负电荷，运动方向与电流方向相反即向左，根据左手定则判断洛伦兹力方向竖直向上，即负电荷向M板偏转，M板带负电荷为低电势，选项A错。由于负电荷向M板集中，使得MN之间形成一个匀强电场，使得自由电子不仅受到洛伦兹力还受到电场力，当二力平衡时，带电粒子不再偏转此时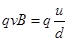，自由电子定向移动的速度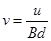选项C正确，根据电流I的微观表达式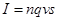，导体单位体积内自由电子数越多，定向移动的速度越小，带入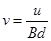，电压越小选项B错。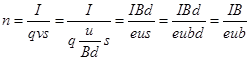对照选项D正确。

本题难度：一般

5、计算题  （15分）如图甲所示，两平行金属板间接有如图乙所示的随时间t变化的交流电压u，金属板间电场可看做均匀、且两板外无电场，板长L=0.2m，板间距离d=0.1m，在金属板右侧有一边界为MN的匀强磁场，MN与两板中线OO′ 垂直，磁感应强度 B=5×10－3T，方向垂直纸面向里。现有带正电的粒子流沿两板中线OO′连续射入电场中，已知每个粒子的比荷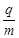=108C/kg，重力忽略不计，在0-0.8×10－5s时间内两板间加上如图乙所示的电压（不考虑极板边缘的影响）。已知t = 0时刻进入两板间的带电粒子恰好在0.2×10－5s时刻经极板边缘射入磁场。（不考虑粒子间相互影响及返回板间的情况）。
求：

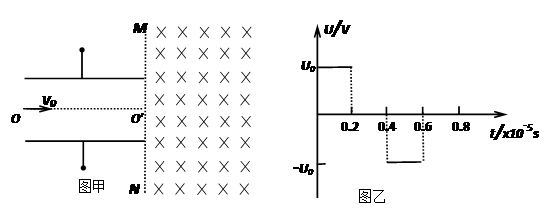
（1）求两板间的电压U0
（2）0-0.2×10－5s时间内射入两板间的带电粒子都能够从磁场右边界射出，求磁场的最大宽度
（3）若以MN与两板中线OO′ 垂直的交点为坐标原点，水平向右为x轴，竖直向上为y轴建立二维坐标系，请写出在0.3×10－5s时刻射入两板间的带电粒子进入磁场和离开磁场（此时，磁场只有左边界，没有右边界）时的位置坐标。
（4）两板间电压为0，请设计一种方案：让向右连续发射的粒子流沿两板中线OO′射入，经过右边的待设计的磁场区域后，带电粒子又返回粒子源。

参考答案：（1）250 V/m（2）0.2 m（3）若向上偏转：进入坐标为 (? 0? ;? 0.0125 ) (m)
离开磁场左边界坐标为 (? 0 ;? 0.4125 ) (m)?若向下偏转：进入坐标为 (? 0? ;? - 0.0125 ) (m)?离开磁场左边界坐标为 (? 0 ;? 0.3875) (m)?（4）见解析

本题解析：(1) （3分）电荷在电场中作类平抛运动?
d/2=at2/2 （1分）? a="d/" t2=2.5×1010 ?(m/s2)
Eq="ma?" （1分） E=ma/q=2.5×1010/108 ="250" (V/m)
U0="Ed=250×0.1=25" (V)?（1分）
(2) （3分） 在0---0.2×10-5S时间内, 0.2×10-5S时刻射入两板间的带电粒子进入磁场并能够从磁场右边界射出,则其他粒子也都能从磁场的右边界射出。粒子进入磁场作匀速圆周运动，则：
Bqv=mv2/R1? R1=mv0/Bq?（1分）
由第一问可知：v0=L/t=0.2/0.2×10-5 =105 (m/s)?（1分）
R1=105/5×10-3×108="0.2" (m)?
磁场的最大宽度为? D=R1=0.2 (m)?（1分）
(3) （7分） 0.3×10-5S时刻进入的粒子先做匀速直线运动,再做类平抛运动. 类平抛运动时间应为t=0.1×10-5S .
若向上偏转,根据平抛运动公式得: y1=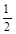at2=2.5×1010×(0.1×10-5)2/2="0.0125" (m) （1分）
进入坐标为 (? 0? ;? 0.0125 ) (m)?（1分）
进入磁场作匀速圆周运动,? R2="mv/Bq"
离开磁场时的坐标 y2=y1+2R2cosθ=y1+2 mv0/Bq
y2=0.0125+2×105/5×10-3×108="0.4125" (m)（1分）
离开磁场左边界坐标为 (? 0 ;? 0.4125 ) (m)?（1分）
若向下偏转,根据平抛运动公式得: y1=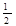at2=2.5×1010×(0.1×10-5)2/2="0.0125" (m)
进入坐标为 (? 0? ;? - 0.0125 ) (m)?（1分）
进入磁场作匀速圆周运动,? R2="mv/Bq"
离开磁场时的坐标 y2= 2R2cosθ- y1=" 2" mv0/Bq- y1
y2=2×105/5×10-3×108-0.0125="0.3875(m)" （1分）
离开磁场左边界坐标为 (? 0 ;? 0.3875) (m) （1分）
(4) （2分）(只要合理均给分)

本题难度：一般