1、计算题  如图1所示，一个质量m＝0.1 kg的正方形金属框总电阻R＝0.5 Ω，金属框放在表面绝缘的斜面AA′B′B的顶端(金属框上边与AA′重合)，自静止开始沿斜面下滑，下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与BB′重合)，设金属框在下滑过程中的速度为v，与此对应的位移为x，那么v2-x图象如图2所示，已知匀强磁场方向垂直斜面向上，金属框与斜面间的动摩擦因数μ＝0.5，取g＝10 m/s2，sin53°＝0.8，cos53°＝0.6。
(1)根据v2-x图象所提供的信息，计算出金属框从斜面顶端滑至底端所需的时间t；
(2)求出斜面AA′B′B的倾斜角θ；
(3)求匀强磁场的磁感应强度B的大小。

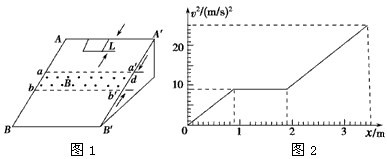
参考答案：解：(1)由v2-x图象可知：
x1＝0.9 m，v1＝3 m/s，做匀加速运动；
x2＝1.0 m，v1＝3 m/s，做匀速运动；
x3＝1.6 m，末速度v2＝5 m/s，做匀加速运动
设线框在以上三段的运动时间分别为t1、t2、t3
则x1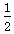＝v1t1，所以t1＝0.6 s
x2＝v1t2，所以t2＝s
x3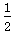＝(v1＋v2)t3，t3＝0.4 s
t＝t1＋t2＋t3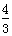＝s
(2)线框加速下滑时，由牛顿第二定律得mgsinθ－μmgcosθ＝ma
由a＝5.0 m/s2得θ＝53°
(3)线框通过磁场时，线框做匀速直线运动，线框受力平衡
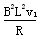＋μmgcosθ＝mgsinθ
线框的宽度L＝d＝0.5x2＝0.5 m
得B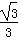＝T

本题解析：

本题难度：困难

2、计算题  （10分）有一绝缘的、半径为R的光滑圆轨道固定在竖直平面内，在其圆心处固定一带正电的点电荷，现有一质量为m，带电量也为正电（其电量远小于圆心处的电荷，对圆心处电荷产生的电场影响很小，可忽略）的小球A，圆心处电荷对小球A的库仑力大小为F。开始小球A处在圆轨道内侧的最低处，如图所示。现给小球A一个足够大的水平初速度，小球A能在竖直圆轨道里做完整的圆周运动。

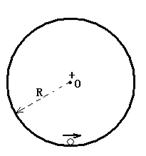
（1）小球A运动到何处时其速度最小？为什么？
（2）要使小球A在运动中始终不脱离圆轨道而做完整的圆周运动，小球A在圆轨道的最低处的初速度应满足什么条件？

参考答案：（1）小球运动到轨道最高点时速度最小，理由见解析 （2）

本题解析：（1）小球运动到轨道最高点时速度最小? 2分
在圆心处电荷产生的电场中，圆轨道恰好在它的一个等势面上，小球在圆轨道上运动时，库仑力不做功，当小球运动到圆轨道最高处时，其重力对它做的负功最多，此时速度最小。? 2分
（2）在最低点，小球受到的电场力F与重 91eXAm.org力mg方向相同，小球不会脱离轨道。
在最高点，小球受到的电场力F与重力mg方向相反，当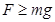时，在最高点小球也不会脱离轨道。此时，小球在最高点的速度v应满足：v>0?（1）? 1分
小球从圆轨道最底处运动到最高处的过程中由动能定理得：
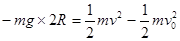?（2）? 1分
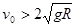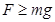由二式解得：?这就是在条件下，小球在最低点速度应满足的条件。? 1分
在最高点，当时，小球在最高点的速度v 应满足：
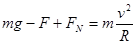?（FN为轨道对小球的支持力）?（3）? 1分
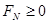?（4）? 1分
由（2）、（3）和（4）可得：?这就是在条件下，小球在最低点速度应满足的条件。?1分

本题难度：一般

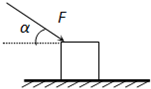
3、简答题  如图所示，质量为m=4kg的物体放在粗糙的水平面上，物体与水平面间的动摩擦因数为μ=0.2，物体在方向与水平面成α=37°斜向下、大小为20N的推力F作用下，从静止开始运动，sin37°=0.6，cos37°=0.8，g=10m/s2．若5s末撤去F，求：
（1）5s末物体的速度大小；
（2）前8s内物体通过的位移大小．

参考答案：（1）物体受力如图所示，据牛顿第二定律有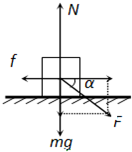
竖直方向上 N-mg-Fsinα=0
水平方向上 Fcosα-f=ma
又 f=μN
解得 a=Fcosθ-μ(mg+Fsinθ)m=1.4m/s2
则5s末的速度大小υ5=at1=1.4×5m/s=7.0m/s
（2）前5s内物体的位移s1=12at12=17.5m
撤去力F后，据牛顿第二定律有-f′=ma′
N′-mg=0
又f′=μN′
解得a′=-μg=-2m/s2
由于t止=-υ5a′=-7.0-2s=3.5s＞t2=（8-5）s=3s
故s2=υ5t2+12a′t22=12m
则前8s内物体的位移大小s=s1+s2=29.5m
答：（1）5s末物体的速度大小为7m/s．
（2）前8s内物体通过的位移大小为29.5m．

本题解析：

本题难度：一般

4、选择题  如图，质量为m的小球与轻质弹簧Ⅰ和水平轻绳Ⅱ相连，Ⅰ、Ⅱ的另一端分别固定于P、Q，当仅剪断Ⅰ、Ⅱ中的一根的瞬间，球的加速度a应是

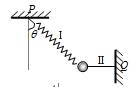
A．若剪断Ⅰ，则a=g，竖直向下
B．若剪断Ⅱ，则a=g tan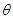，方向水平向左
C．若剪断Ⅰ，则a=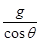，方向沿Ⅰ的延长线
D．若剪断Ⅱ，则a=g，竖直向上

参考答案：AB

本题解析：分析：弹簧的形变是明显形变，因而本题中，刚剪短细绳时，弹簧来不及形变，故弹簧弹力不能突变；细绳的形变是微小形变，在刚剪短弹簧的瞬间，细绳弹力可突变！
解答：解：绳子未断时，受力如图，由共点力平衡条件得，T2=mgtanθ，T1=．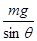

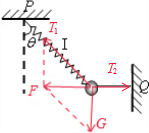
刚剪短弹簧Ⅰ瞬间，细绳弹力突变为0，故小球只受重力，加速度为g，竖直向下，故A正确，C错误；
刚剪短细线瞬间，弹簧弹力和重力不变，受力如图

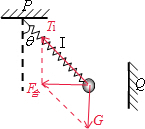
由几何关系，F合=T1sinθ=T2=ma，因而a=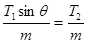，因而B正确，D错误；
故选A、B．
点评：本题为瞬时问题，弹簧弹力不可突变，细绳弹力可突变！

本题难度：简单

5、选择题  如图在密封的盒子内装有一个质量为m的金属球，球刚能在盒内自由活动，若将盒子在空气中竖直向上抛出，抛出后上升、下降的过程中(空气阻力不能忽略) (? )

A．上升过程球对盒底有压力，下降过程球对盒顶有压力
B．上升过程球对盒顶有压力，下降过程球对盒底有压力
C．上升，下降过程中球均对盒底有压力
D．上升，下降过程中球均对盒无压力

参考答案：B

本题解析：盒子在空中运动过程中，由于盒外空气阻力不能忽略，盒内没有空气，上升和下降过程中盒子受到与运动方向相反的阻力，同样的时间，上升的高度小，故选项B正确。

本题难度：一般