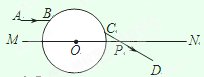
1、计算题  （10分）如图，一透明球体置于空气中，球半径R＝10cm，折射率n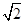＝?．MN是一条通过球心的直线，单色细光束AB平行于MN射向球体，B为入射点，AB与MN间距为5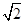?cm，CD为出射光线．
（1）补全光路并求出光从B点传到C点的时间；
（2）求CD与MN所成的角α．（写出求解过程）

参考答案：(1) t=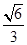?10-9s．(2)α=30°

本题解析：1）连接BC，如图?（2分）

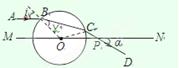
在B点光线的入射角、折射角分别为i、γ，
sini=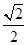?．所以，i=45°?（2分）
由折射定律：在B点有n=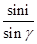?，（1分）
sinγ=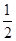?，故γ=30°；?（2分）
BC=2Rcosγ，v=?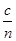
t=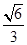10-9s．?（1分）
（2）由几何关系可知∠COP=15°，∠OCP=135°，α=30°?（2分）

本题难度：一般

2、填空题  在用插针法测定玻璃砖折射率的实验中，一同学在纸上画出玻璃砖界面ab、cd，在插了4枚大头针后画出了光路图，如图中①所示，测得的玻璃砖的折射率可表示为______（用图中给出的字母表示）．若该同学在实验中，插大头针P3、P4时不小心使玻璃砖向下发生了平移，如图中②所示，但是他依然用原来画的边界画了光路图，他测出的折射率与玻璃砖折射率相比______．（“偏大”“偏小”或“相同”）

参考答案：

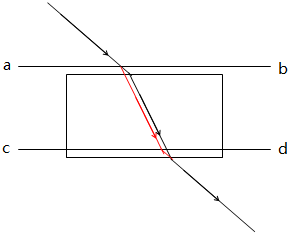
根据折射定律可知，玻璃砖的折射率可表示为n=sinisinr．
如右图所示，黑线表示玻璃砖向下平移后实际的光路图，红线表示作图光路图，由图看出，黑线与红线平行，说明画图时的入射角、折射角与实际的入射角、折射角相等，由折射定律可知，测出的折射率与玻璃砖折射率相比相同．
故答案为：sinisinr，相同

本题解析：

本题难度：一般

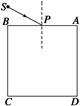
3、计算题  （10分）在真空中有一正方体玻璃砖，其截面如图所示，已知它的边长为d.在AB面上方有一单色点光源S，从S发出的光线SP以60°入射角从AB面中点射入，当它从侧面AD射出时，出射光线偏离入射光线SP的偏向角为30°，若光从光源S到AB面上P点的传播时间和它在玻璃砖中传播的时间相等，求点光源S到P点的距离。

参考答案：L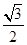＝d（

本题解析：（10分）光路图如图所示，由折射定律知，光线在AB面上折射时有n＝（1分）
在BC面上出射时n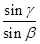＝（1分）

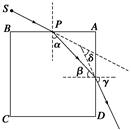
由几何关系有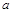＋β＝90°（1分）
δ＝(60°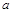－)＋(γ－β)＝30°（1分）
联立以上各式并代入数据解得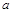＝β＝45°，γ＝60°（1分）
所以n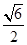＝（1分）
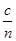光在棱镜中通过的距离s＝d＝t（2分）
设点光源到P点的距离为L，有L＝ct（1分）
解得L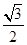＝d（1分）

本题难度：一般

4、选择题  光从空气进入某介质，当入射角是53°时，折射角为37°；则当入射角为0°时的折射角和介质的折射率分别是（sin37°=0.6，sin53°=0.8）（　　）
A．0°和0
B．0°和1
C．0°和1.33
D．90°和0.75

参考答案：根据折射定律得：n=sin53°sin37°=43=1.33．当入射角为0°时，则折射角为0°．故C正确，A、B、D错误．
故选C．

本题解析：

本题难度：简单

5、简答题  如图所示，是一种液体深度自动监测仪示意图，在容器的底部水平放置一平面镜，在平面镜上方有一光屏与平面镜平行．激光器发出的一束光线以60°的入射角射到液面上，进入液体中的光线经平面镜反射后再从液体的上表面射出，打在光屏上形成一亮点，液体的深度变化后光屏上亮点向左移动了2

参考答案：

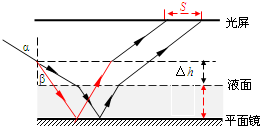
设入射角为α，折射角为β，原来液面深度为h，液面深度增加△h，屏上光点移动的距离
s=2

本题解析：

本题难度：一般