1、计算题  某种透明物质制成的直角三棱镜ABC，折射率为n,角A等于30°。一细束光线在纸面内从O点射入棱镜，如图所示，当入射角为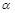时，发现刚好无光线从AC面射出，光线垂直于BC面射出。求：

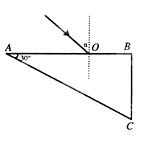
①透明物质的折射率n。
②光线的入射角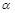。（结果可以用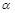的三角函数表示）

参考答案：①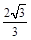②

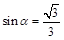
本题解析：：①由题意可知，光线射向AC面恰好发生全反射，反射光线垂直于BC面从棱镜射出，光路图如下图。
设该透明物质的临界角为C，由几何关系可知

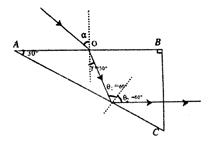
C=θ1=θ2=60°,sinC=1/n,
解得n=。…………………………………（1分）
②由几何关系得：r=30°……（1分）
由折射定律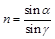…………………（1分）
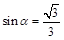……………………………（1分）

本题难度：一般

2、选择题  “不经历风雨怎么见彩虹”，彩虹的产生原因是光的色散，如图所示为太阳光射到空气中的小水珠发生色散形成彩虹的光路示意图，a、b为两种折射出的单色光。以下说法正确的是

[? ]
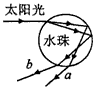
A．a光光子能量大于b光光子能量
B．在水珠中a光的传播速度小于b光的传播速度
C．用同一双缝干涉装置看到的a光干涉条纹间距比b光宽
D．如果b光能使某金属发生光电效应，则a光也一定能使该金属发生光电效应

参考答案：C

本题解析：

本题难度：一般

3、简答题  如图所示为ABC是三角形玻璃砖的横截面，∠ABC=90°，∠BAC=30°，一束平行于AB的光束从AC边射入玻璃砖，EF是玻璃砖中的部分光路，且EF与AC平行，则玻璃砖的折射率为______，光束______（填“能”或“不能”）从F点射出玻璃砖．

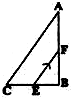
参考答案：作出光路图，根据几何知识得：i=60°．
因EF∥AC，光线在BC面上发生反射，根据反射定律和几何知识可知，r=30°
则折射率 n=sinisinr=sin60°sin30°=

本题解析：

本题难度：一般

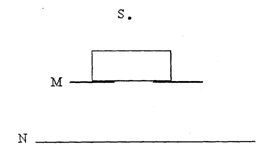
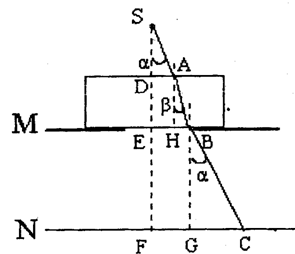
4、简答题  如图所示：水平放置的纸板M上有直径8cm的圆孔，光屏N与M相距6cm，点光源S在圆孔中心正上方相距6cm处，在纸板上面放一厚度为cm的玻璃砖（盖住整个圆孔）时，光屏上光斑直径为20cm，求玻璃板的折射率？

参考答案：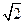

本题解析：
如图所示：

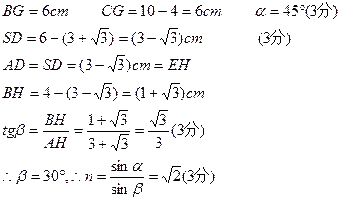
本题难度：简单

5、简答题  某同学为了测量截面为正三角形的玻璃三棱镜折射率，进行了如下实验．
a．用刻度尺在白纸上画一条直线，在所画直线的适当位置处插入两枚大头针P1、P2，然后将三棱镜的一条边AC与所画直线重合．调节三棱镜所放位置，使CP1=AP2，并画出三棱镜AB、BC的界面；
b．在AB界面左侧透过三棱镜观察P1，调整视线的方向，直至大头针P1的像被P2挡住，然后在AB界面左侧再插上第三枚大头针P3，使P2挡住P1的像和P3，记下P1、P2、P3的位置；
c．将三棱镜换一个底面，重复步骤a、b各再测一次；
d．处理数据，计算折射率．
（1）如图是该同学在白纸上留下的实验痕迹，请在答题卷的图上将光路补充完整；
（2）为测出三棱镜玻璃的折射率，若以AB作为分界面，只需要用量角器测量一个角，这个角是______（请在图上用符号标出），则该玻璃三棱镜的折射率是n=______．

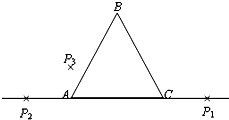
参考答案：（1）由题意可知，P3P2的连线即为折射光线，由于CP1=AP2，根据几何对称性，可得：入射光线的入射点与折射光线的出射点连线与AC平行，则光路图如下所示；
（2）由上图可知，只需要用量角器测量一个角，这个角是θ；由几何关系，则有：θ入=30°；
根据光的折射定律，由于光线是从光密介质进入光疏介质，则有：n=sinθsin30°=2sinθ；
故答案为：（1）光路图如上图所示；
（2）θ（如图）；2sinθ．

本题解析：

本题难度：一般