1、计算题 如图所示,质量M=3.0kg的平板小车静止在光滑水平面上,当t=0时,两个质量均为m=1.0kg的小物体A和B(均可视为质点),分别从左端和右端以水平速度v1=4.0m/s和v2=2.0m/s冲上小车,当它们在车上停止滑动时,A、B没有相碰。A、B与车面的动摩擦因数均为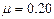 ,g取10m/s2。
,g取10m/s2。

小题1:求A、B在车上停止滑动时车的速度;
小题2:车的长度至少是多少;
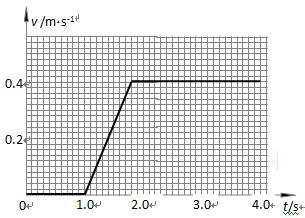
小题3:在图所给出的坐标系中画出0至4.0s内小车的速度—时间图象。
参考答案:
小题1:0.40m/s方向水平向右
小题2:4.8m
小题3:
本题解析:(1)设A、B在车上停止滑动时,车的速度为v,根据动量守恒定律有:
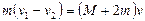 ……………………………………………………………………(2分)
……………………………………………………………………(2分)
解得? v = 0.40m/s……………………………………………………………………(1分)
方向水平向右。…………………………………………………………………………(1分)
(2)设A、B在车上相对于车滑动的距离分别为l1和l2,由功能关系有:
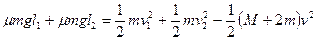 ?……………………………(2分)
?……………………………(2分)
解得: l1+l2=4.8m,即车长至少为4.8m。………………………………………………(2分)
(3)车的运动分以下三个阶段:
第一阶段:A、B同时在车上滑行时,滑块对车的摩擦力均为μmg,方向相反,车受力平衡而保持不动。当B的速度减为0时,此过程结束。设这段时间内滑块的加速度为a,根据牛顿第二定律有: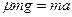 ,解得滑块的加速度
,解得滑块的加速度  。
。
滑块B在小车上相对滑行的时间为? =1.0s。…………………………(1分)
=1.0s。…………………………(1分)
第二阶段:B停止运动后,A继续在车上滑行,设到t2时刻物体A与车有共同速度v,则? v=v1-at2,
解得:t2=1.8s。…………………(1分)
第三阶段:t2之后,车以速度v做匀速直线运动。到t=4.0s为止,物体的速度时间图线如图答所示。………………(2分)

本题难度:一般
2、计算题 质量为m="0.2" kg的小球从水平地面处以20m/s的速度竖直上抛,能上升的最大高度为16m,然后落回水平地面,与水平地面发生碰撞后再次上升,上升的高度为7 m。而后又落回水平地面…,直到最后静止在水平地面上,设小球受到的空气阻力大小恒定,g取 10 m/s2,求:
(1) 小球所受空气阻力的大小
(2) 小球第一次上升时间和第一次下落时间之比
(3) 从小球刚开始上抛到第二次即将落到水平地面上之前的过程中损失的机械能
参考答案:(1) 小球第一次上升过程中,由动能定理得: - (mg + f)h1 =" 0" -  mvo2?
mvo2?
代入数据解得(2 + f )×16 =  ×0.2×202?∴? f =" 0.5" N?
×0.2×202?∴? f =" 0.5" N?
(2) 小球第一次上升过程中加速度大小为
a1 = (mg + f )/m = (2 + 0.5)/0.2 =" 12.5" m/s2?
得上升所用时间为:? t1 = 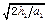 ?
?
小球第一次下落过程中加速度大小为:
a2 = (mg - f)/m = (2 - 0.5)/0.2 =" 7.5" m/s2?
得下落所用时间为: t2 =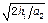 ?∴?时间之比为 :t1/t2 =
?∴?时间之比为 :t1/t2 = 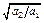 ?=
?=  ?
?
(3) 第一次落回地面时的速度大小为 v1,则 2 f h1 =  m(vo2 - v12)?
m(vo2 - v12)?
解得 v1 = 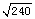 ?m/s?设第二次上升时初速度为 v2 ,?
?m/s?设第二次上升时初速度为 v2 ,?
则 (mg + f )h2 = m v22?解得 v2 = 5
m v22?解得 v2 = 5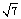 m/s?小球与地面撞击时损失的能量?
m/s?小球与地面撞击时损失的能量?
?E1 =  mv12 -
mv12 -  mv22 =
mv22 =  ×0.2×(240 - 175)=" 6.5" J?
×0.2×(240 - 175)=" 6.5" J?
小球在空气中损失的机械能为
?E2 = f(2h1 + 2h2) = 0.5×(2×16 + 2×7) ="?" 23 J?
从小球刚开始上抛到第二次落到平面之前的过程中损失的机械能为
?E = ?E1 +?E2 = f(2h1 + 2h2)+ mv12 -
mv12 - mv22 =" 23" + 6.5 =" 29.5" J?
mv22 =" 23" + 6.5 =" 29.5" J?
也可以先求出第二次落回地面时速度的大小 v3,则有:(mg – f )h2 = m v32?
m v32?
∴? mv32 = (0.2×10 - 0.5)×7 =" 10.5"
mv32 = (0.2×10 - 0.5)×7 =" 10.5"
则 ?E =  mvo2 –
mvo2 – m v32 =
m v32 =  ×0.2×202 - 10.5 =" 40" - 10.5 =" 29.5" J
×0.2×202 - 10.5 =" 40" - 10.5 =" 29.5" J
本题解析:略
本题难度:简单
3、计算题 如图甲所示,一条轻质弹簧左端固定在竖直墙面上,右端放一个可视为质点的小物块,小物块的质量为m=1.0 kg,当弹簧处于原长时,小物块静止于O点。现对小物块施加一个外力F,使它缓慢移动,将弹簧压缩至A点,压缩量为x=0.1 m,在这一过程中,所用外力F与压缩量的关系如图乙所示。然后撤去F释放小物块,让小物块沿桌面运动,已知O点至桌边B点的距离为L=2x,水平桌面的高为h=5.0m,计算时,可用滑动摩擦力近似等于最大静摩擦力。(g取10 m/s2) 求:
(1)在压缩弹簧过程中,弹簧存贮的最大弹性势能;
(2)小物块落地点与桌边B的水平距离。

参考答案:解:(1)取向左为正方向,从F-x图中可以看出,小物块与桌面间的滑动摩擦力大小为Ff=1.0 N,方向为负方向 ①
在压缩过程中,摩擦力做功为Wf=-Ff·x=-0.1 J?②
由图线与x轴所夹面积可得外力做功为WF=(1.0+47.0)×0.1÷2 J=2.4 J?③
所以弹簧存贮的弹性势能为Ep=WF+Wf=2.3 J?④
(2)从A点开始到B点的过程中,由于L=2x,摩擦力做功为Wf"=Ff"3x=0.3 J?⑤
对小物块用动能定理有 ?⑥
?⑥
解得vB=2 m/s?⑦
物块从B点开始做平抛运动 ?⑧
?⑧
下落时间t=1 s
水平距离s=vBt=2 m?⑨
本题解析:
本题难度:一般
4、计算题 如图所示,一小物块从倾角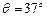 的斜面上的A点由静止开始滑下,最后停在水平面上的C点。已知小物块的质量m = 0.10kg,小物体与斜面和水平面间的动摩擦因数均为μ=0.25,A点到斜面底部B点的距离L = 0.50m,斜面与水平面平滑连接,小物块滑过斜面与水平面连接处时无机械能损失。求:
的斜面上的A点由静止开始滑下,最后停在水平面上的C点。已知小物块的质量m = 0.10kg,小物体与斜面和水平面间的动摩擦因数均为μ=0.25,A点到斜面底部B点的距离L = 0.50m,斜面与水平面平滑连接,小物块滑过斜面与水平面连接处时无机械能损失。求:
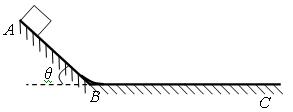
(1) 小物块在斜面上运动时的加速度大小;
(2) BC间的距离;
(3) 若在C点给小物块一水平初速度使小物块恰能回到A点,此初速度为多大?(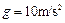 )
)
参考答案::(1) 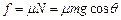 ,
,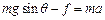
所以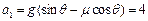 m/s2
m/s2
(2) 由功能关系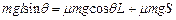 ,S = 0.8m
,S = 0.8m
(3) 由动能定理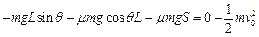 ,
,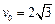 m/s
m/s
本题解析:略
本题难度:简单
5、计算题 如图所示,在光滑水平面上有两个木块A和B,其质量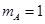 ?kg
?kg 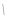 ,
,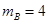 ?kg,它们中间用一根轻质弹簧相连。一颗水平飞行的子弹质量为
?kg,它们中间用一根轻质弹簧相连。一颗水平飞行的子弹质量为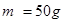 ,以
,以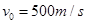 的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的
的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的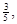 且子弹射穿A木块损失的动能是射穿B木块损失的动能的2倍。求:系统运动过程中弹簧的最大弹性势能。
且子弹射穿A木块损失的动能是射穿B木块损失的动能的2倍。求:系统运动过程中弹簧的最大弹性势能。 
参考答案:22.5 J
本题解析:子弹穿过A时,子弹与A动量守恒,由动量守恒定律得:
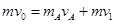 ?①
?①
而由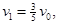 则
则 ?m/s
?m/s
解得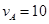 ?m/s?②
?m/s?②
子弹穿过B时,子弹与B动量守恒,由动量守恒定律得:
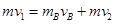 ?③
?③
又由 ?④
?④
解得 ?
?
由③④解得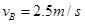
子弹穿过B以后,弹簧被压缩,A、B和弹簧所组成的系统动量守恒,当A、B速度相等时,弹簧有最大弹性势能,有动量守恒定律得:
 ?⑥
?⑥
由功能关系得:
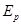
 ?⑦
?⑦
由②⑤⑥⑦解得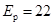 .5 J。
.5 J。
点评:本题主要考查了动量守恒定律及能量关系的直接应用,要求同学们能正确分析运动过程,明确过程中哪些量守恒,难度较大.
本题难度:一般