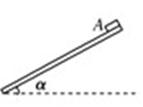
1、选择题  如右图所示，长为L的长木板水平放置，在木板的A端放置一个质量为m的小物块．现缓慢地抬高A端，使木板以左端为轴转动，当木板转到与水平面的夹角为α时小物块开始滑动，此时停止转动木板，小物块滑到底端的速度为v，则在整个过程中(　　)

A．支持力对物块做功为0
B．支持力对小物块做功为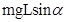
C．摩擦力对小物块做功为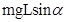
D．滑动摩擦力对小物块做功为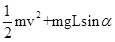

参考答案：B

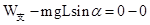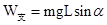本题解析：物块在缓慢提高过程中，由动能定理可得：，则有．故A错误 B正确；物块在缓慢提高过程中，静摩擦力始终与运动方向垂直，所以静摩擦力不做功，故C错误；物块在滑动过程中，由动能定理可得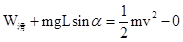：，则有滑动摩擦力做功为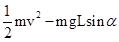．故D错误；
故选B
点评：当力是恒定时，除可由力与力的方向位移求出功外，还可以由动能定理来确定；当力是变化时，则只能由动能定理来求出力所做的功．

本题难度：一般

2、简答题  一宠物毛毛狗“乐乐”在玩耍时不慎从离地h1=19.5m高层阳台无初速度竖直掉下，当时刚好是无风天气，设它的质量m=2kg，在“乐乐”开始掉下的同时，几乎在同一时刻刚好被地面上的一位保安发现并奔跑到达楼下，奔跑过程用时2.5s，恰好在距地面高度为h2=1.5m处接住“乐乐”，“乐乐”缓冲到地面时速度恰好为零，设“乐乐”下落过程中空气阻力为其重力的0.6倍，缓冲过程中空气阻力为其重力的0.2倍，重力加速度g=10m/s2．求：
（1）为了营救“乐乐”允许保安最长的反应时间；
（2）在缓冲过程中保安对“乐乐”做的功．

参考答案：（1）对“乐乐”用牛顿第二定律mg-0.6mg=ma1求得：a1=4m/s2?
“乐乐”下落过程：h1-h2=12a1t2
求得：t=3s?
允许保安最长反应时间：t=（3-2.5）s=0.5s?
（2）“乐乐”下落18m时的速度υ1=a1t=12m/s?
缓冲过程中，对“乐乐”由动能定理得：W+mgh2-0.2mgh2=0-12mυ12
解得：W=-168J?
答：（1）为了营救“乐乐”允许保安最长的反应时间为0.5s；（2）在缓冲过程中保安对“乐乐”做的功-168J．

本题解析：

本题难度：一般

3、选择题  真空中存在范围足够大、竖直方向的匀强电场，A、B为该匀强电场中的两个等势面。现有三个质量相同、带同种等量电荷的小球a、b、c，从等势面A上的某点同时以相同速率v0分别沿竖直向下、水平向右和竖直向上方向开始运动，如图所示。经过一段时间，三个小球先后通过等势面B，则下列判断正确的是

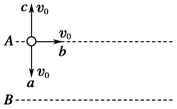
A．等势面A的电势一定高于等势面B的电势
B．a、c两小球通过等势面B时的速度相同
C．开始运动后的任一时刻，a、b两小球的动能总是相同
D．开始运动后的任一时刻，三个小球电势能总是相等

参考答案：B

本题解析：由于小球所受重力和电场力的大小不知，所以电场的方向不确定，即AB两等势面电势的高低不确定，A错；对a、b、c三小球通过等势面B时，电场力和重力对三球做功相同，所以三球通过等势面B时的动能相同，而ac在水平方向没有速度，所以ac两球在竖直方向的速度相同，B对；开始运动后a球由于具有向下的初速度，所以要比b球向下运动的快，即重力和电场力对ab两球做功不同，所以在任一时刻，a、b两小球的动能不相同，C错；因在任一时刻三球在竖直方向的位移不同，所以电场力做功不同，即三球的电势能不相等，D错。
点评：本题学生做时能想象出三球的运动过程，知道在开始运动后任一时刻在竖直方向上的速度和位移都不同。

本题难度：一般

4、选择题  如图所示，用平行于斜面的拉力F拉着木箱沿粗糙斜面加速向上移动。下列说法中正确的是

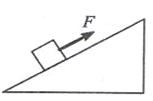
A．拉力F对木箱所做的功等于木箱增加的动能与木箱克服摩擦力所做的功之和
B．拉力F对木箱所做的功等于木箱克服摩擦力所做的功与克服重力所做的功之和
C．拉力F对木箱所做的功等于木箱增加的机械能
D．拉力F对木箱所做的功等于木箱增加的机械能与木箱克服摩擦力所做的功之和

参考答案：D

本题解析：在木箱移动过程中，受重力、斜面的支持力、摩擦力及拉力作用．这四个力中，有重力、拉力和摩擦力做功．重力做负功使重力势能增加，摩擦力做负功产生热能．因为物体加速运动，根据动能定理，合力做的功等于动能的增量．而机械能等于动能与重力势能之和，故F做的功等于木箱增加的动能与重力势能以及克服摩擦力所做的功的和，所以ABC错误，D正确
故选：D．

本题难度：一般

5、计算题  如图所示，质量为m＝0.1 kg可视为质点的小球从静止开始沿半径为R1＝35 cm的圆弧轨道AB由A点滑到B点后，进入与AB圆滑连接的1/4圆弧管道BC.管道出口处为C，圆弧管道半径为R2＝15 cm，在紧靠出口C处，有一水平放置且绕其水平轴线匀速旋转的圆筒(不计筒皮厚度)，筒上开有小孔D，筒旋转时，小孔D恰好能经过出口C处，若小球射出C出口时，恰好能接着穿过D孔，并且还能再从D孔向上穿出圆筒，小球到最高点后返回又先后两次向下穿过D孔而未发生碰撞，不计摩擦和空气阻力，g取10 m/s2，问：

(1)小球到达B点的瞬间前后对轨道的压力分别为多大？
(2)小球到达C点的速度多大？
(3)圆筒转动的最大周期T为多少？

参考答案：(1) N′1＝N1＝3 N；N′2＝N2＝5.7 N? (2) 0.2 s.?1分

本题解析：(1)AB过程机械能守恒：mgR1＝mvB2　vB＝m/s? 2分
到达B点瞬间前：N1－mg＝m? 1分
到达B点瞬间后：N2－mg＝m? 1分
依牛顿第三定律，对轨道的压力大小分别为N′1＝N1＝3 N；N′2＝N2＝5.7 N? 2
(2)小球向上穿过圆筒D孔又从D孔向上穿出所用的时间t1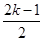＝T(k＝1、2、3……)；
小球向上穿出D孔后竖直上抛又返回到D孔进入圆筒所用时间为2t2＝nT(n＝1、2、3……)又由竖直上抛规律有：0＝vC－g(t1＋t2)? 1分
所以T＝? 2?分
当k＝n＝1时T有最大值，所以T＝0.2 s.? 1分
本题考查动能定理和圆周运动规律的应用，在B点为圆周运动的一部分，由支持力和重力的合力提供向心力，由动能定理可求得B点速度大小，再由向心力公式求得支持力大小，由A到C应用动能定理可求得C点速度大小，由于圆筒转动的周期性，经过半个周期的奇数倍时物体能从C点穿出，于是得到周期T的表达式，由此N=1时周期最大

本题难度：一般