1、简答题
粒子弹以水平速度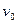 击中木块A并留在其中,子弹打入木块的过程持续时间极短,可
击中木块A并留在其中,子弹打入木块的过程持续时间极短,可
不考虑此过程中木块A的移动。已知木块A的质量为(M-m),木B的质量为M,子
弹的质量为m,弹簧原长为L0,劲度系数为k,弹簧的弹性势能与形变量的对应关系为
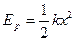 .如果此后运动过程中弹簧始终处于弹性限度内,且A、B不会发生直接碰触。试求:
.如果此后运动过程中弹簧始终处于弹性限度内,且A、B不会发生直接碰触。试求:
(1)当弹簧压缩到最短时,B的速度大小;
(2)运动中弹簧出现的最大长度。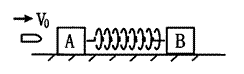
参考答案:(1)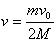 (2)
(2)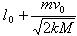
本题解析:(1)子弹打入木块以及木块运动的整个过程中,子弹和两木块组成的系统
动量守恒。当弹簧压缩到最短时,A、B的速度相等,设为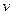 ?
?
则: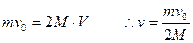
(2)子弹打入木块A的过程中,子弹和A组成的系统动量守恒
设二者共同速度为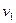 ,则
,则 ……(1)
……(1)
当弹簧达到最大长度时两木块速度相等,由动量宗教恒定律得: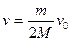 ……(2)
……(2)
从子弹射入木块A有共同速度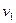 以后的A、B运动过程中,系统机械能守恒,故
以后的A、B运动过程中,系统机械能守恒,故
 ……(3)
……(3)
弹簧的最大长度为:L= ……(4)
……(4)
评分细则:第(1)问解答正确得6分,第(2)问得出式①和②各得3分,得出式③
和结果得4分,得出式④得2份。
本题难度:一般
2、计算题 (21分)在倾角为30°的光滑斜面上有相距40m的两个可看作质点的小物体P和Q,质量分别mP=0.1kg和mQ=0.5kg,其中P不带电,Q带电。整个装置处在正交的匀强电场和匀强磁场中,电场强度的大小为50V/m,方向竖直向下;磁感应强度的大小为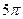 T,方向垂直纸面向里。开始时,将小物体P无初速释放,当P运动至Q处时,与静止在该处的小物体Q相碰,碰撞中Q的电荷量保持不变(即不转移)。碰撞后,两物体能够再次相遇。斜面无限长,g取10m/s2。求:
T,方向垂直纸面向里。开始时,将小物体P无初速释放,当P运动至Q处时,与静止在该处的小物体Q相碰,碰撞中Q的电荷量保持不变(即不转移)。碰撞后,两物体能够再次相遇。斜面无限长,g取10m/s2。求:
(1)试分析物体Q的带电性质并求出电荷量大小;
(2)分析物体P、Q第一次碰撞后物体Q可能的运动情况,此运动是否为周期性运动?若是,物体Q的运动周期为多大?
(3)物体P、Q第一次碰撞结束后瞬间P、Q的速度大小各是多少
参考答案:(1)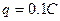 且物体Q带负电
且物体Q带负电
(2)2s
(3)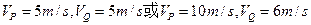
本题解析:
(1)对物体Q,在碰撞之前处于静止状态,由平衡条件知:
 (2分)?得
(2分)?得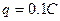 且物体Q带负电(2分)
且物体Q带负电(2分)
(2)物体P、Q碰撞之后,物体Q受重力、电场力、洛伦兹力的作用,由于重力和电场力等大反向,故物体Q将在斜面上方做匀速圆周运动. (2分)
对物体Q?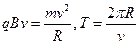 ?(2分)
?(2分)
匀速圆周运动的周期?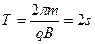 (2分)
(2分)
(3)要使P、Q能够再次相遇,则相遇点一定为P、Q的第一次碰撞点,物体P在碰撞后一定反向弹回,再次回到碰撞点时再次相遇。
对物体P,从释放到与Q碰撞之前,由运动学公式 有:
有:
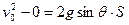 ?得
?得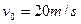 ?(2分)
?(2分)
对物体P和Q,在碰撞过程中,动量守恒有
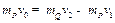 (2分)
(2分)
对物体P,时间关系: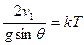 ? (
? (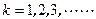 )(2分)
)(2分)
当k=1时, ,
,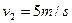 ,(1分)
,(1分)
当k=2时, ,
,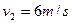 ,(1分)
,(1分)
当k=3时, ,
,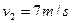 ,系统总动能增加不满足能量守恒定律。
,系统总动能增加不满足能量守恒定律。
同理分析可知K只能取1、2,综上所述碰撞过程结束后P、Q的速度可能是
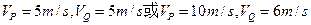 。(3分)
。(3分)
本题难度:一般
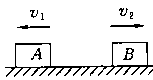
3、计算题 如图所示,A、B均置于水平面上,其与水平面间的动摩擦因数之比为1︰2,分别向左、右运动。若A、B组成的系统动量守恒,则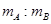 为多少?若它们同时停下,其初速度之比
为多少?若它们同时停下,其初速度之比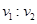 为多少?
为多少?
参考答案: ,负号说明A、B速度方向相反
,负号说明A、B速度方向相反
本题解析:由动量守恒的条件可得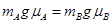 所以
所以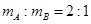 。
。
它们同时停下,说明系统的总动量为零,即A、B动量大小相等、方向相反有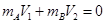 ,代入得,
,代入得, ,负号说明A、B速度方向相反。
,负号说明A、B速度方向相反。
本题难度:简单
4、选择题 质量为m的物体静止在光滑水平面上,从t = 0时刻开始受到水平拉力的作用力的大小F与时间t的关系如图所示,力的方向保持不变,则(?)
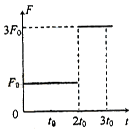
A.t0时刻的瞬时速度为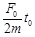
B.在t = 0到t0这段时间内拉力做功为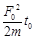
C.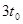 时刻拉力的瞬时功率为
时刻拉力的瞬时功率为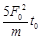
D.在t = 0到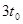 这段时间内,拉力的平均功率为
这段时间内,拉力的平均功率为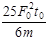
参考答案:D
本题解析:由动量定理可知在0-t0时间内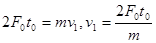 ,A错;t=t0时刻,根据动量定理可知此时速度为
,A错;t=t0时刻,根据动量定理可知此时速度为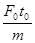 ,由动能定理拉力做功为
,由动能定理拉力做功为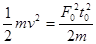 ,B错;在
,B错;在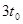 时刻根据动量定理求得瞬时速度
时刻根据动量定理求得瞬时速度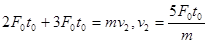 ,瞬时功率P=
,瞬时功率P= ,C错;物体动能增量为
,C错;物体动能增量为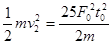 ,即为拉力做的功,平均功率为
,即为拉力做的功,平均功率为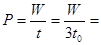
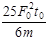 ,D对;
,D对;
本题难度:简单
5、计算题 如图所示,轻弹簧的两端与质量均为2m的B、C两物块固定连接,静止在光滑水平面上,物块C紧靠挡板但不粘连.另一质量为m的小物块A以速度V0从右向左与B发生弹性正碰,碰撞时间极短可忽略不计.(所有过程都在弹簧弹性限度范围内)求:
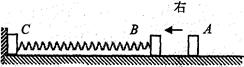
(1)A、B碰后瞬间各自的速度;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比.
参考答案:(1)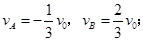 (2)
(2)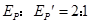
本题解析:(1)A、B发生弹性正碰,碰撞过程中,A、B组成的系统动量守恒、机械能守恒,以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得: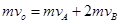 ,
,
在碰撞过程中机械能守恒,由机械能守恒定律得: 联立解得:
联立解得: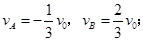
(2)弹簧第一次压缩到最短时,B的速度为零,该过程机械能守恒,由机械能守恒定律得,弹簧的弹性势能: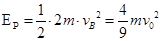 ,
,
从弹簧压缩最短到弹簧恢复原长时,B、C与弹簧组成的系统机械能守恒,弹簧恢复原长时,B的速度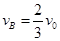 ,速度方向向右,C的速度为零,
,速度方向向右,C的速度为零,
从弹簧恢复原长到弹簧第一次伸长最长时,B、C与弹簧组成的系统动量守恒、机械能守恒,弹簧伸长最长时,B、C速度相等,以向右为正方向,由动量守恒定律得: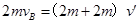 ,
,
由机械能守恒定律得: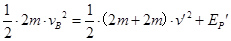 ,解得:
,解得: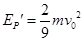 ,
,
弹簧第一次压缩最短与第一次伸长最长时弹性势能之比: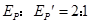 ;
;
考点:考查了机械能守恒,动量守恒,
本题难度:一般