1、选择题  一个质量为1kg的物体被人用手由静止向上提升1m ，这时物体的速度是2m/s ，则下列说法中正确的是（g=10m/s2）：
[? ]
A、手对物体做功12J
B、合外力对物体做功12J
C、合外力对物体做功2J
D、物体克服重力做功10J

参考答案：ACD

本题解析：

本题难度：简单

2、填空题  木块受水平力F作用在水平面上由静止开始运动，前进s后撤去F，木块又沿原方向前进3s停止，则摩擦力f=________，木块最大动能为________。

参考答案：，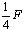

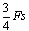
本题解析：

本题难度：一般

3、简答题  某学校科技小组对一辆自制小遥控车的性能进行研究，他们让小车在水平地面上由静止开始运动，并将小车运动的全过程记录下来，通过数据处理得到如图所示的v-t图象，已知小车在0-2s内做匀加速直线运动，2-10s内小车牵引力的功率保持不变，在10s末停止遥控，关闭电动机．小车的质量m=1kg，整个过程中小车受到的阻力保持不变．求：
（1）小车所受的阻力f；
（2）小车在2-10s内牵引力的功率；
（3）小车在14s内阻力f做的功．

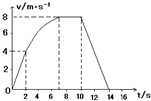
参考答案：（1）在7～10s内小车匀速运动故F=f，所以P=Fv=fvmax=8f，
而在0～2s内小车的加速度a=△v△t=42=2m/s2，
根据牛顿第二定律可知：F合=ma，
即F-f=ma，
所以：F=f+ma=f+1×2=f+2，
故在t=2s时有：P=（f+2）×4，
由于在2～10s内牵引力的功率保持不变，
所以f×8=（f+2）×4，
解得：f=2N．
（2）t=10s时牵引力的功率P=Fv=2×8=16W；
（3）摩擦力在0～2s内所做的功为：W1=-fx1=-2×4×22=-8J，
根据动能定理2～10s对小车有：P△t+W2=12mv2-12mv22，
解得：W2=-P△t+12mv2-12mv22=-16×8+12×1×（64-16）=-128+24=-104J，
在10～14s时间内小车做匀减速运动，其加速度a′=fm=-22=-1m/s2，
所以在t=14s时物体的速度v3=0，
故在10～14s内阻力对小车所做的功为：W3=-2×8+02×4=-32J，
故0～14s内摩擦阻力对小车所做的功为：W=W1+W2+W3=-8-104-32=-144J．
答：（1）小车所受的阻力为2N；（2）小车在2-10s内牵引力的功率为16W；（3）小车在14s内阻力f做的功为-144J．

本题解析：

本题难度：一般

4、简答题  光滑水平地面上停放着一辆质量m=2kg的平板车，质量M=4kg可视为质点的小滑块静放在车左端，滑块与平板车之间的动摩擦因数μ＝0.3，如图所示．一水平向右的推力F＝24N作用在滑块M上0.5s撤去，平板车继续向右运动一段时间后与竖直墙壁发生碰撞，设碰撞时间极短且车以原速率反弹，滑块与平板之间的最大静摩擦力与滑动摩擦力大小相等，平板车足够长，以至滑块不会从平板车右端滑落，g取10m/s2．求：

（1）平板车第一次与墙壁碰撞后能向左运动的最大距离s多大？此时滑块的速度多大？
（2）平板车第二次与墙壁碰撞前的瞬间速度v2多大？
（3）为使滑块不会从平板车右端滑落，平
板车l至少要有多长？

参考答案：（1）0.33m；（2）0.67m/s；（3）1m

本题解析：（1）滑块与平板车之间的最大静摩擦力fm=μMg，设滑块与车不发生相对滑动而一起加速运动的最大加速度为am，以车为研究对象，则am=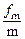= =6m/s2
以滑块和车整体为研究对象，作用在滑块上使滑块与车一起静止地加速的水平推力的最大值设为Fm，则Fm=(M+m)am＝36N
已知水平推力F=24N<36N，所以在F作用下M、m能相对静止地一起向右加速．
设第一次碰墙前M、m的速度为v1，v1==2m/s
第一次碰墙后到第二次碰前车和滑块组成的系统动量守恒
车向左运动速度减为0时，由于m<M，滑块仍在向右运动，设此时滑块的速度为v1"，车离墙壁距离s
Mv1－mv1=Mv1"
v1"＝=1m/s
以车为研究对象，根据动能定理，有－μMgs＝－mv12
s==0.33m
（2）第一次碰撞后车运动到速度为零时，滑块仍有向右的速度，滑动摩擦力使车以相同的加速度重新向右加速，如果车的加速过程持续到与墙第二次相碰，则加速过程位移也为s，可算出第二次碰鲡瞬向的速度大小也为2m/s，系统的总动量将大于第一次碰墙后的动量，这显然是不可能的，可见在第二次碰墙前车已停止加速，即第二次碰墙前一些时间车和滑块已相对静止．
设车与墙壁第二次碰撞前瞬间速度为v2，则Mv1－mv1=(M+m)v2
v2=v1=0.67m/s
（3）车每次与墙碰撞后一段时间内，滑块都会相对车有一段向右的滑动，由于两者相互摩擦，系统的部分机械能转化为内能，车与墙多次碰撞后，最后全部机械能都转化为内能，车停在墙边，滑块相对车的总位移设为l，则有
μMgl＝(M+m)v12
代入数据解得l=1m

本题难度：一般

5、计算题  如图所示，光滑绝缘竖直细杆与以正点电荷O为圆心的圆周交于B、C两点。一质量m、带电量为-q的空心小球从杆上A点无初速下落。设AB =" BC" = h，小球滑到B点的速度为试求：

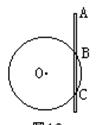
（1）小球滑至C点的速度；
（2）A、C两点的电势差。

参考答案：（1）（2）

本题解析：(1)BC两点是等式点，从B到C过程中，电场力做功为零，由B至C过程，应用动能定理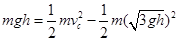：?(2分)解得? 1分)
（2）由A→B应用动能定理，解得（2分）
点评：关键是知道BC两点处于同一个等势面上

本题难度：一般