1、简答题  如图所示，在直角区域aob内，有垂直纸面向里的匀强磁场，一对正、负电子从o点沿纸面以相同速度射入磁场中，速度方向与边界ob成30°角，求正、负电子在磁场中运动的时间之比．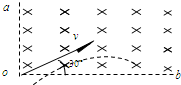

参考答案：

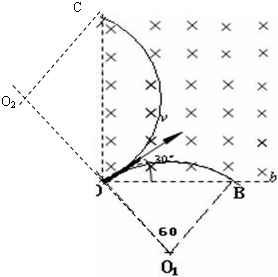
由evB=mv2R，则有? 半径R=mveB，周期T=2πmeB，则知正负电子在磁场中运动的相同的周期．
由左手定则判断得知，正电子向上偏转，负电子向下偏转，根据几何知识得，正电子轨迹对应的圆心角∠OO2C=120°，
运动时间为t1=120°360°T=13T
负电子轨迹对应的圆心角为∠OO1B=60°，运动时间为
? t2=60°360°T=16T
则正、负电子在磁场中运动的时间之比为t1：t2=2：1．
答：正、负电子在磁场中运动的时间之比为t1：t2=2：1．

本题解析：

本题难度：一般

2、填空题  内壁光滑的环形细圆管，位于竖直平面内，环的半径为R（比细管的半径大得多）．在细圆管中有两个直径略小于细圆管管径的小球（可视为质点）A和B，质量分别为m1和m2，它们沿环形圆管（在竖直平面内）顺时针方向运动，经过最低点时的速度都是v0；设A球通过最低点时B球恰好通过最高点，此时两球作用于环形圆管的合力为零，那么m1、m2、R和v0应满足的关系式是______．

参考答案：（1）A球通过最低点时，作用于环形圆管的压力竖直向下，根据牛顿第三定律，A球受到竖直向上的支持力N1，由牛顿第二定律，有：
N1-m1g=m1v02R…①
由题意知，A球通过最低点时，B球恰好通过最高点，而且该时刻A、B两球作用于圆管的合力为零；可见B球作用于圆管的压力肯定竖直向上，根据牛顿第三定律，圆管对B球的反作用力N2竖直向下；假设B球通过最高点时的速度为v，则B球在该时刻的运动方程为：
N2+m2g=m2v2R…②
由题意有：N1=N2…③
得：m1g+m2g=m2v2R-m1v02R…④
对B球运用机械能守恒定律有：12m2v02=12m2v2+2m2gR…⑤
解得：v2=v02-4gR…⑥
⑥式代入④式可得：(m1+5m2)g+(m1-m2)v02R=0．
故答案为：(m1+5m2)g+(m1-m2)v02R=0．

本题解析：

本题难度：一般

3、选择题  物体做匀速圆周运动时，下列说法中不正确的是（　　）
A．向心力一定指向圆心
B．向心力一定是物体受到的合外力
C．向心力的大小一定不变
D．向心力的方向一定不变

参考答案：A、物体做匀速圆周运动时，向心力始终指向圆心，大小不变，故A正确；
B、做匀速圆周运动的物体，合外力提供向心力，故B正确；
C、由于是匀速圆周运动向心力F=mv2r大小不变，故C正确；
D、匀速圆周运动物体，向心力方向时刻在变，故D错误．
本题选择错误的，故选D．

本题解析：

本题难度：一般

4、选择题  质量不计的轻质弹性杆P插在桌面上，杆上端套有一个质量为m的小球，今使小球在水平面内做半径为R的匀速圆周运动，角速度为ω，如图所示，则杆的上端受到的作用力大小是

[? ]
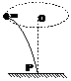
A、mRω2?
B、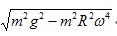
C、
D、不能确定

参考答案：C

本题解析：

本题难度：一般

5、简答题  如图所示，直角坐标系xoy所决定的平面内，在平行于x轴的虚线MN上方、x＜0的区域存在着沿x轴正方向的匀强电场；在x＞0的某区域存在方向垂直于坐标平面的圆形有界匀强磁场（图中未画出）．现有一比荷k=

参考答案：（1）带电粒子在匀强电场中y轴方向上做匀速直线运动，x轴方向上做匀加速直线运动，将O点的速度分解，有：
cosθ=v0v=12．
解得θ=60°．
（2）根据动能定理得，qU=12mv2-12mv02
因为比荷k=qm=102C/kg
代入数据解得：U=6V．
（3）根据qvB=mv2R
带电粒子在匀强磁场中的轨道半径：R=mvqB=401.2×1100=13m．
根据几何关系得：x=R+Rsin30°=3R=1m．
（4）以粒子在匀强磁场中运动的轨迹的初末两点连线为圆的直径，该圆的面积为匀强磁场的最小面积．
该圆的半径r=Rsin60°=

本题解析：

本题难度：一般