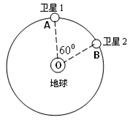
1、选择题  北斗导航系统又被称为“双星定位系统”，具有导航、定位等功能。计划“北斗”系统最终将有5颗静止轨道卫星和30颗非静止轨道卫星组成。这些卫星均绕地心O做匀速圆周运动。某时刻两颗正在同时提供服务的非静止轨道卫星分别位于轨道上的A、B两位置（如图所示）．若卫星均顺时针运行，轨道半径为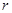，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力．则以下判断中错误的是（? )

A．这两颗卫星的加速度大小相等，均为
B．卫星1由位置A运动到位置B所需的时间为
C．卫星1由位置A运动到位置B的过程中万有引力做功为零
D．卫星1向后喷气就一定能追上卫星2

参考答案：D

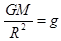本题解析：根据万有引力提供向心力：：解得：①；而②
由①②解得卫星的加速度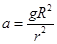：，故A正确．
根据万有引力提供向心力，所以卫星1由位置A运动到位置B所需的时间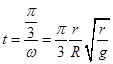，故B正确．
卫星在运动的过程中万有引力与速度方向垂直，不做功，故C正确．
卫星1加速后万有引力不够提供向心力，做离心运动，会离开原来的圆轨道，D错误
让选错误的故选D
点评：解决本题的关键掌握万有引力提供向心力，以及黄金代换式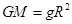，把要求解的物理量先表示出来即可．

本题难度：一般

2、选择题  2013年2月16日凌晨，2012DAl4小行星与地球“擦肩而过”，距离地球最近约2．77万公里。据观测，它绕太阳公转的周期约为366天，比地球的公转周期多1天。假设小行星和地球绕太阳运行的轨道均为圆轨道，对应的轨道半径分别为R1、R2，线速度大小分别为 v1、v2，向心加速度分别为a1、a2，表面重力加速度分别为g1、g2，以下关系式正确的是
A．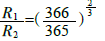
B．?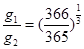
C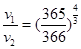
D．

参考答案：A

本题解析：小行星和地球都绕太阳运动，根据开普勒第三定律则有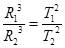，即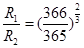，选项A对。万有引力提供向心力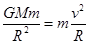，线速度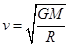，所以小行星和地球绕太阳运行的线速度之比,选项C错。向心加速度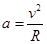，可得小行星和地球绕太阳运行的向心加速度之比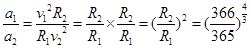，选项D错。小行星和地球表面的重力加速度需要找到小行星和地球的质量半径，题目中没有提供相关信息，无法计算，选项B错。

本题难度：一般

3、选择题  已知地球质量大约是月球质量的81倍，地球半径大约是月球半径的4倍．不考虑地球、月球自转的影响，由以上数据可推算出地球表面重力加速度与月球表面重力加速度之比约为(? )
A．9：8
B．9：4
C．81：16
D．81：4

参考答案：C

本题解析：根据万有引力等于重力表示出重力加速度得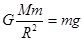：，即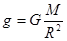，其中R为星球半径，M为星球质量．所以地球表面重力加速度与月球表面重力加速度之比约为81：16．故C正确．
点评：求一个物理量之比，我们应该把这个物理量先用已知的物理量表示出来，再进行之比．

本题难度：一般

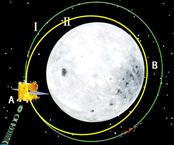
4、选择题  2010年10月1日，“嫦娥二号”卫星发射成功。作为我国探月工程二期的技术先导星，“嫦娥二号”的主要任务是为“嫦娥三号”实现月面软着陆开展部分关键技术试验，并继续进行月球科学探测和研究。如图所示，“嫦娥二号”卫星的工作轨道是100km环月圆轨道Ⅰ，为对“嫦娥三号”的预选着陆区——月球虹湾地区（图中B点正下方）进行精细成像，“嫦娥二号”在A点将轨道变为椭圆轨道Ⅱ，使其近月点在虹湾地区正上方B点，大约距月面15km。下列说法中正确的是?
?
A．沿轨道Ⅱ运动的周期小于沿轨道Ⅰ运动的周期
B．在轨道Ⅱ上A点的加速度等于在轨道Ⅰ上A点的加速度
C．在轨道Ⅱ上A点的速度大于在轨道Ⅰ上A点的速度
D．完成任务后，卫星返回工作轨道Ⅰ时，在A点需加速

参考答案：ABD

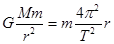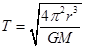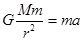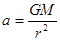本题解析：由公式得，半径越大，周期越大，故沿轨道Ⅱ运动的周期小于沿轨道Ⅰ运动的周期，A正确，由公式得，故在轨道Ⅱ上A点的加速度等于在轨道Ⅰ上A点的加速度，B正确，由公式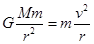得，故在轨道Ⅱ上A点的速度等于在轨道Ⅰ上A点的速度，C错误，当由低轨道向高轨道运动时需要加速逃逸，所以D正确，
故选ABD
点评：本题是卫星类型的问题，常常建立这样的模型：环绕天体绕中心天体做匀速圆周运动，

本题难度：一般

5、填空题  太阳对行星的作用力是?力，方向?

参考答案：万有引力；由行星指向太阳

本题解析：太阳对行星的作用力是万有引力，方向是由行星指向太阳，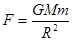
故答案为：万有引力；由行星指向太阳

本题难度：简单