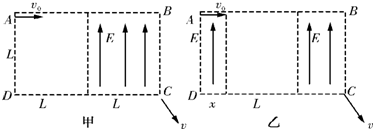
1、简答题  如图所示，在长为2L、宽为L的ABCD区域内有一半的空间存在场强为E、方向平行于BC边的匀强电场，现有一个质量为m，电量为e的电子，以平行于AB边的速度v0从区域的左上角A点射入该区域，不计电子所受的重力，则：
（1）当无电场的区域位于左侧时（如图甲），求电子射出ABCD区域时的动能；
（2）当无电场区域的左边界距AD的距离为x时（如图乙），要使这个电子能从区域的右下角的C点射出，电子的初速度v0应满足什么条件．

参考答案：
（1）电子先做匀速运动，进入电场后做类平抛运动，设电子恰好从C点射出电场．
? 电子在电场中运动的加速度a=eEm
设电子恰好从C点射出电场时在电场中的运动时间为t，则有
? L=v0t，L=12at2
解得：v0=

本题解析：

本题难度：一般

2、选择题  平抛运动可以分解为水平和竖直方向的两个直线运动，在同一坐标系中作出这两个分运动的v－t图线，如图所示。若平抛运动的时间大于2t1，下列说法中正确的是?（?）

参考答案：A

本题解析：平抛运动水平方向是匀速，竖直方向是自由落体运动，图线b的斜率代表重力加速度g，A正确；t1时刻的水平速度与竖直速度大小相等，所以t1时刻的速度方向与初速度方向夹角为45?，B错误；2t1时刻的竖直速度大小为初速度的2倍，故2t1时刻的动能是初动能的5倍，C错误；0~t1时间内的竖直位移与t1~2t1时间内的竖直位移之比为1∶3，故两段时间内重力做功之比为1∶3，重力的功率之比也为1∶3，D错误。

本题难度：简单

3、选择题  对平抛运动的物体，若g已知，再给出下列哪组条件，可确定其初速度大小（　　）
A．水平位移
B．下落高度
C．落地时速度大小和方向
D．落地时位移大小和方向

参考答案：知道末速度大小和方向，只要将末速度正交分解到水平和竖直方向，水平方向的分速度就等于初速度，所以C正确；
知道末位移大小和方向，则将末位移分解到水平和竖直方向，由竖直位移和g求时间，再用水平位移除以时间，就得到了初速度，所以D正确．
故选CD．

本题解析：

本题难度：简单

4、计算题  在倾角为37°的斜面上，从A点以6m/s的速度水平抛出一小球，小球落在B点，如图所示，求小球刚落到斜面时的速度方向，AB两点间距离和小球在空中飞行时间。（g=10m/s）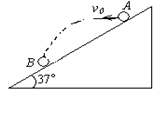

参考答案：arctan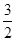

本题解析：小球落到B点时速度偏角为α，运动时间为t，则：
tan37°=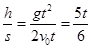?又因为tan37°=?
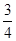解得t=0.9s? B两点间水平距离S=v0t=6×0.9m=5.4m
A．B两点间距离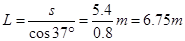
在B点时，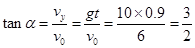
所以，小球捧到斜面时速度方向与水平方向间的夹角为arctan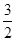
本题考查平抛运动规律的应用,小球落在斜面上根据位移与水平方向成37°角,把位移分解为水平分位移和竖直分位移,由竖直方向和水平方向的分运动列公式,由tan37°求解运动时间,再由分运动求得水平位移和竖直位移，由勾股定理求得合位移

本题难度：一般

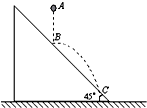
5、简答题  如图所示，固定斜面倾角为45°，从斜面上方A点处由静止释放一个质量为m的弹性小球，在B点处和斜面碰撞，碰撞后速度大小不变，方向变为水平，经过一段时间在C点再次与斜面碰撞．已知AB两点的高度差为h，重力加速度为g，不考虑空气阻力．求：BC间的竖直高度H．

参考答案：小球下降过程中，做自由落体运动，落到斜面B点的速度为v，
满足：2gh=v2
解得：v=

本题解析：

本题难度：一般