|
高中物理知识点大全《对单物体(质点)的应用》高频试题强化练习(2019年最新版)(六)
2019-06-28 05:13:10
【 大 中 小】
|
1、计算题 如图所示,半径为r=20cm的两圆柱A和B,靠电动机带动按同方向均以8rad/s的角速度匀速转动,两圆柱的转动轴互相平行且在同一平面内,转动方向图中已标出,质量均匀的木棒放置其上,重心开始恰在B的上方,棒和圆枉体间的动摩擦因数为0.16,图中s=1.6m,L>2m,重力加速度取l0m/s2,从捧开始运动到重心恰在A上方需要时间为多少?

参考答案:从棒开始运动到重心恰在A上方的时间为t ="t" 1 + t 2 =1.5s
本题解析:木棒左移过程中受A、B两轮的摩擦力,f=fA+fB=μ(NA+NB)=μmg此时木棒的加速度
a="f/m=μ" g=1.6m/s。
A、B圆柱边缘的线速度v="r" ω =0.2×8m/s=1.6m/s,木棒被加速到与圆柱边缘线速度相同的时间
tl =v/a=1.6/1.6 s="1" s
此过程中木棒与圆柱边缘有相对滑动,木棒向左位移sl=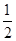 at 12 =0.8m at 12 =0.8m
而后木棒与圆柱边缘没有相对滑动,与圆柱体边缘一起向左匀速运动的位移
s2=s-s1=1.6m-0.8m=0.8m,再匀速至重心到A上的时间t2=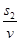 = =  s = 0.5s. s = 0.5s.
从棒开始运动到重心恰在A上方的时间为t ="t" 1 + t 2 =1.5s
考点:本题考查了牛顿第二定律,匀变速直线运动位移与时间的关系
本题难度:一般
2、选择题 如图所示,质量均为 的木块A和B,用劲度系数为 的木块A和B,用劲度系数为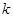 的轻质弹簧连接,最初系统静止.用大小 的轻质弹簧连接,最初系统静止.用大小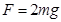 、方向竖直向上的恒力拉A直到B刚好离开地面,则在此过程中 、方向竖直向上的恒力拉A直到B刚好离开地面,则在此过程中
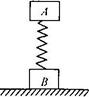
A.A上升的初始加速度大小为2g
B.弹簧对A和对B的弹力是一对作用力与反作用力
C.A上升的最大高度为
D.A上升的速度先增大后减少
|
参考答案:A
本题解析:A.最初系统静止,则A受到的重力和弹力是一对平衡力,施加F的瞬间,其合外力与F等大,由牛顿第二定律可得,加速度为2g,故A正确;B.弹簧对A和对B的弹力的施力物体都是弹簧,受力物体分别是A和B两个物体,所以不是作用力与反作用力,故B错误; C.直到B刚好离开地面这一过程中A上升的高度是弹簧压缩和拉伸的形变量之和,即2mg/k,故C错误;D.在运动的过程中,因为F=2mg,所以A所受到的合外力一直向上,所以速度一直增大,故D错误。故选A。
考点:本题考查了共点力的平衡条件、牛顿第二定律、胡可定律.
本题难度:一般
3、计算题 (8分)如图,光滑半圆弧轨道半径为r,OA为水平半径,BC为竖直直径。水平轨道CM与C点相切,轨道上有一轻弹簧,一端固定在竖直墙上,另一端恰位于轨道的末端C点(此时弹簧处于自然状态)。一质量为m的小物块自A处以竖直向下的初速度v0=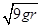 滑下,到C点后压缩弹簧进入水平轨道,被弹簧反弹后恰能通过B点。重力加速度为g,求: 滑下,到C点后压缩弹簧进入水平轨道,被弹簧反弹后恰能通过B点。重力加速度为g,求:

(1)物块通过B点时的速度大小;
(2)物块离开弹簧刚进入半圆轨道C点时对轨道的压力大小;
(3)弹簧的最大弹性势能。
参考答案:(1)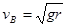 (2)6mg (3)EP=4mgr (2)6mg (3)EP=4mgr
本题解析:(1)物块恰能通过B点,即此时对轨道的压力为零:
解得: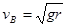
(2)物块由C点到B点机械能守恒:
在C点:
由以上三式联立可得FN=6mg
由牛顿第三定律可知,物块对轨道最低点的压力为6mg
(3)物块从A点到弹簧最短过程中,根据能量守恒定律: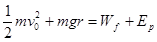
物块从弹簧最短到B点过程,根据能量守恒: 
解得EP=4mgr。
考点:本题考查能量守恒定律
本题难度:一般
4、计算题 如图所示,质量M=8.0kg、长L=2.0m的薄木板静置在水平地面上,质量m=0.50kg的小滑块(可视为质点)以速度v0=3.0m/s从木板的左端冲上木板。已知滑块与木板间的动摩擦因数μ=0.20,重力加速度g取10m/s2。

(1)若木板固定,滑块将从木板的右端滑出,求:
a.滑块在木板上滑行的时间t;
b.滑块从木板右端滑出时的速度v。
(2)若水平地面光滑,且木板不固定。在小滑块冲上木板的同时,对木板施加一个水平向右的恒力F,如果要使滑块不从木板上掉下,力F应满足什么条件?(假定滑块与木板之间最大静摩擦力与滑动摩擦力相等)
参考答案:(1)a.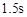 b.1m/s(2) b.1m/s(2)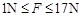
本题解析:(1)a.滑块在木板上做匀减速直线运动,初速度为v0=3.0m/s,位移为L=2.0m。滑块在滑行的过程中受重力、支持力、和摩擦力,其中重力=支持力。根据牛顿第二定律有,滑块加速度的大小
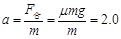 m/s2 m/s2
设滑块在木板上滑行的时间为t,根据运动学公式有
所以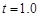 s 或 s 或 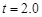 s(舍) (3分) s(舍) (3分)
之所以要舍去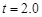 s,是因为如果木板足够长,当 s,是因为如果木板足够长,当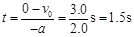 s时,滑块就静止了。 s时,滑块就静止了。
b. m/s (2分) m/s (2分)
(2)①设当F=F1时,滑块恰好运动到木板的右端,然后与木板一起运动。在滑块与木板有相对滑动的这段时间内,滑块做匀减速直线运动,木板做匀加速直线运动。设这段时间为t1,滑块与木板共同运动的速度为v1,则有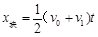 , ,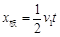 , ,
所以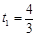 s, s,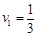 m/s m/s
所以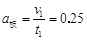 m/s2 m/s2
根据牛顿第二定律有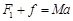
所以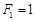 N N
所以,当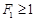 N时,滑块不会从木板的右端滑出 (4分) N时,滑块不会从木板的右端滑出 (4分)
②当滑块与木板共速后,只要不发生相对滑动,滑块就不会从木板的左端滑出,根据牛顿第二定律:滑块与木板共同运动的加速度 ,而滑块在静摩擦力的作用下,能达到的最大加速度 ,而滑块在静摩擦力的作用下,能达到的最大加速度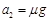 。因此,滑块不从木板左端滑出需满足的条件是 。因此,滑块不从木板左端滑出需满足的条件是 ,即 ,即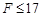 N。 (3分) N。 (3分)
所以滑块不从木板掉下的条件是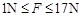 。 。
考点:考查了牛顿第二定律与运动学公式的应用
本题难度:困难
5、计算题 如图所示,x轴与水平传送带重合,坐标原点0在传送带的左端,传送带OQ长 L=8m,传送带顺时针速度V。=5m/s, —质量m=1kg的小物块轻轻放在传送带上xp="2m" 的P点,小物块随传送带运动到Q点后恰好能冲上光滑圆弧轨道的最高点N点。小物块与 传送带间的动摩擦因数μ.=0.5,重力加速度g= 10m/s2,求:
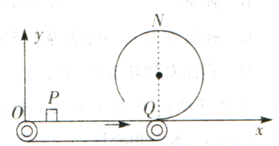
(1)N点的纵坐标;
(2)若将小物块轻放在传送带上的某些位置,小物块均能沿光滑圆弧轨道运动(小物块始终 在圆弧轨道运动不脱轨)到达纵坐标yM=0.25m的M点,求这些位置的横坐标范围。
参考答案:(1)yN=1m;(2)7m≤x≤7 .5m和0≤x≤5 .5m
本题解析:(1)小物块在传送带上匀加速运动的加速度a=μg=5m/s2
小物块与传送带共速时,所用时间
运动的位移
故小物块与传送带达到相同速度后以v0=5m/s的速度匀速运动到o,然后冲上光滑圆弧轨道恰好到达N点,故有:
由机械能守恒定律得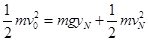
解得yN=1m
(2)设在坐标为x1处将小物块轻放在传送带上,若刚能到达圆心右侧的M点,由能量守恒得:
μmg(L-x1)=mgyM 代入数据解得x1=7.5 m
μmg(L-x2)=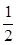 mgyN 代入数据解得x2=7 m mgyN 代入数据解得x2=7 m
若刚能到达圆心左侧的M点,由(1)可知x3=5.5 m
故小物块放在传送带上的位置坐标范围为
7m≤x≤7 .5m和0≤x≤5 .5m
考点:牛顿第二定律;机械能守恒定律;能量守恒定律.
本题难度:困难
|