1、计算题  一质量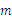＝2.0 kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面，某同学利用传感器测出了小物块从一开始冲上斜面到之后上滑过程中多个时刻的瞬时速度，并用计算机作出了小物块上滑过程的速度—时间图线，如图所示。物块的最大静摩擦力等于滑动最大静摩擦力（取＝0.6，cos 37°＝0.8，g取10m/s2）求：

(1)物块冲上斜面过程中的加速度大小和最远距离；
(2)物块与斜面间的动摩擦因数；
(3)判断物块最后能否返回斜面底端？若能返回，求出返回斜面底端过程中的加速度大小；若不能返回，求出物块停在什么位置。

参考答案：（1）10.8m/s2；1.35m.（2）0.6.（3）能下滑; 1.2m/s2

本题解析：（1）物体的加速度：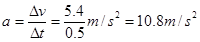
最远距离：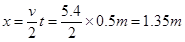
（2）物体冲上斜面过程中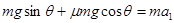：，解得μ=0.6
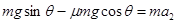（3）滑块速度减为零时，由于，故物体能下滑，下滑的加速度：，解得：a2=1.2m/s2
考点：牛顿第二定律的应用.

本题难度：一般

2、计算题  水平传送带以v=2m/s速度顺时针匀速运动，将物体轻放在传送带的A端，它可以先匀加速后匀速运动到传送带另一端B。传送带AB两端间的距离为L=4m，物体和传送带间的动摩擦因数μ=0.1，g取10m/s2。求：

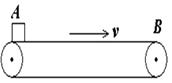
(1)物体在匀加速过程中加速度大小？
(2)物体A端经多长时间运动到B端
(3)若传送带以v=4m/s速度逆时针匀速运动，为使物体仍能到达B端，在A端至少给物体多大的初速度？

参考答案：（1）1m/s2;（2）3s（3）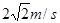

本题解析：(1)物体在匀加速过程中，由牛顿第二定律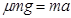：，解得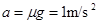
（2）当物块和传送带共速时，经历的时间：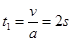
物体的位移：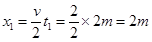
在以后的运动中，到达右端所用的时间：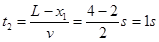
共用时间：t=t1+t2=3s
（3）若传送带以v=4m/s速度逆时针匀速运动，则物体一直减速运动，加速度为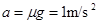，为使物体仍能到达B端，则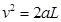，解得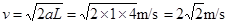
考点：牛顿第二定律的应用；匀变速直线运动的规律.

本题难度：一般

3、计算题  (14分)如图所示，质量M=5kg的木板A在恒力F的作用下以速度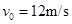向右做匀速度直线运动，某时刻在其右端无初速度地放上一质量为的小物块B．已知木板与地面间的摩擦因数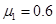，物块与木板间的摩擦因数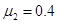．(物块可看作质点，木板足够长，取g=10m/s2)试求：

(1)放上物块后木板发生的位移；
(2)物块与木板之间产生的摩擦热。

参考答案：（1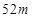）（2）

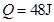
本题解析：（1）可知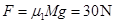                    （1分）
放上物体之后的木板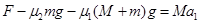：      （1分）
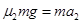物块：      （1分）
令二者速度相等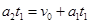：      （1分）
得：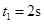
可知速度相同时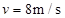：       （1分）
2s内木板发生的位移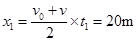：      （1分）
二者共速后一起做匀减速运动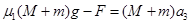：    （1分）
一起做减速运动的时间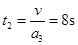：          （1分）
减速过程中木板发生的位移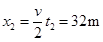：        （1分）
因此木板发生的总位移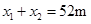        （1分）
（2）在第一个过程中，物块的位移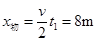        （1分）
物块与木反之间产生的摩擦热为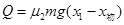：        （2分）
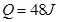得：        （1分）
考点：牛顿第二定律，功能关系，匀变速直线运动公式

本题难度：困难

4、计算题  试用牛顿运动定律推导动量守恒定律

参考答案：

本题解析：令和分别表示两质点的质量，和分别表示它们所受的作用力，和分别表示它们的加速度，和分别表示和F2作用的时间．和分别表水它们相互作用过程中的初速度，和分别表示末速度，由牛顿第二定律得： ①
由加速度的定义可知： ②
把②代入①代入上式，可得： ③
由牛顿第三定律，可知： ④
由③，①可得：③
其中和为两质点的初动量，和为两质点的末动量，这就是动量守恒定律的表达式．
考点：考查了牛顿运动定律，动量守恒定律

本题难度：一般

5、实验题  要测量两个质量不等的沙袋的质量，由于没有直接的测量工具，某实验小组选用下列器材：轻质定滑轮(质量和摩擦可忽略)、砝码一套(总质量m＝0.5 kg)、细线、刻度尺、秒表．他们根据已学过的物理学知识，改变实验条件进行多次测量，选择合适的变量得到线性关系，作出图线并根据图线的斜率和截距求出沙袋的质量．请完成下列步骤．

(1)实验装置如图所示，设右边沙袋A质量为m1，左边沙袋B的质量为m2
(2)取出质量为m′的砝码放在右边沙袋中，剩余砝码都放在左边沙袋中，发现A下降，B上升；（左右两侧砝码的总质量始终不变）
（3）用刻度尺测出A从静止下降的距离h，用秒表测出A下降所用的时间t，则可知A的加速度大小a＝________；
（4）改变m′，测量相应的加速度a，得到多组m′及a的数据，作出________(选填“a­m′” 或“a­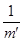”)图线；
（5）若求得图线的斜率k＝4 m/(kg·s2)，截距b＝2 m/s2，则沙袋的质量m1＝________ kg，m2＝________ kg.

参考答案：（3）
(4) a～m′
(5) m1＝3kg，    m2＝1.5kg.

本题解析：（3）由题，质量为m1的沙袋从静止开始下降做匀加速直线运动，由，解得
（5）根据牛顿第二定律得：
对m1及砝码：（m1+△m）g-T=（m1+△m）a
对m2及砝码：T-（m2+m-△m）g=（m2+m-△m）a
联立解得：
根据数学知识得知：“a～△m”成线性关系，图线斜率，截距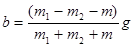
将m=0.5kg，g=10m/s2，k=4m/kg?s2，b=2m/s2，代入解得：m1=3kg，m2=1.5kg．
故答案为：（3）；（5）3，1.5．
考点：利用牛顿第二定律测量两个质量不等的沙袋的质量

本题难度：一般