1、计算题  如图甲所示，表面绝缘、倾角θ=30°的斜面固定在水平地面上，斜面的顶端固定有弹性挡板，挡板垂直于斜面，并与斜面底边平行。斜面所在空间有一宽度D=0.40m的匀强磁场区域，其边界与斜面底边平行，磁场方向垂直斜面向上，磁场上边界到挡板的距离s=0.55m。一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形闭合金属框abcd，放在斜面的底端，其中ab边与斜面底边重合，ab边长L=0.50m。从t=0时刻开始，线框在垂直cd边沿斜面向上大小恒定的拉力作用下，从静止开始运动，当线框的ab边离开磁场区域时撤去拉力，线框继续向上运动，并与挡板发生碰撞，碰撞过程的时间可忽略不计，且没有机械能损失。线框向上运动过程中速度与时间的关系如图乙所示。已知线框在整个运动过程中始终未脱离斜面，且保持ab边与斜面底边平行，线框与斜面之间的动摩擦因数μ=/3，重力加速度g取10?m/s2。
（1）求线框受到的拉力F的大小；
（2）求匀强磁场的磁感应强度B的大小；
（3）已知线框向下运动通过磁场区域过程中的速度v随位移x的变化规律满足v＝v0-（式中v0为线框向下运动ab边刚进入磁场时的速度大小，x为线框ab边进入磁场后对磁场上边界的位移大小），求线框在斜面上运动的整个过程中产生的焦耳热Q。

参考答案：解：（1）由v-t图象可知，在0～0.4s时间内线框做匀加速直线运动，进入磁场时的速度为v1=2.0m/s，所以在此过程中的加速度a=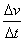=5.0m/s2
由牛顿第二定律F-mgsinθ-μmgcosθ=ma
解得F=1.5 N
（2）由v-t图象可知，线框进入磁场区域后以速度v1做匀速直线运动
产生的感应电动势E=BLv1
通过线框的电流I==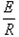
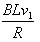
线框所受安培力F安=BIL=
对于线框匀速运动的过程，由力的平衡条件，有F=mgsinθ+μmgcosθ+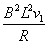
解得B=0.50T
（3）由v-t图象可知，线框进入磁场区域后做匀速直线运动，并以速度v1匀速穿出磁场，说明线框的宽度等于磁场的宽度D=0.40m
线框ab边离开磁场后做匀减速直线运动，到达档板时的位移为s-D=0.15m
设线框与挡板碰撞前的速度为v2
由动能定理，有-mg(s-D)sinθ-μmg(s-D)cosθ=
解得v2=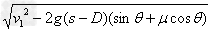=1.0 m/s
线框碰档板后速度大小仍为v2，线框下滑过程中，由于重力沿斜面方向的分力与滑动摩擦力大小相等，即mgsinθ=μmgcosθ=0.50N，因此线框与挡板碰撞后向下做匀速运动，ab边刚进入磁场时的速度为v2=1.0 m/s；进入磁场后因为又受到安培力作用而减速，做加速度逐渐变小的减速运动，设线框全部离开磁场区域时的速度为v3
由v＝v0-得v3= v2-=-1.0 m/s
因v3<0，说明线框在离开磁场前速度已经减为零，这时安培力消失，线框受力平衡，所以线框将静止在磁场中某位置
线框向上运动通过磁场区域产生的焦耳热Q1=I2Rt=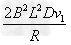=0.40 J
线框向下运动进入磁场的过程中产生的焦耳热Q2=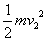 =0.05 J
所以Q=Q1+Q2=0.45 J

本题解析：

本题难度：困难

2、简答题  如图所示，竖直向上的匀强磁场磁感应强度B0=0.5T，并且以

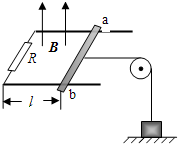
参考答案：（1）感应电流的方向：顺时针绕向?
ε=△?△t=ld△B△t=0.8×0.5×1=0.4V?
感应电流大小：I=εR0+R=0.40.4+0.1=0.8A?
（2）由感应电流的方向可知磁感应强度应增加：B=B0+△B△t?t
安培力?F=BId=(B0+△B△t?t)Id
要提起重物，F≥mg，(B0+△B△t?t)Id=mg
t=(mgId-B0)△B△t=(2×100.8×0.5-0.5)1=49.5?s?
答：（1）感应电流的方向：顺时针绕向以及感应电流的大小为0.8A；
（2）经过49.5s时间能吊起重物．

本题解析：

本题难度：一般

3、选择题  金属导体板宽为d，通以如图所示方向的电流，其中自由电子定向运动的速度为v，整个导体板置于磁感应强度为B的匀强磁场中。则下面说法正确的是

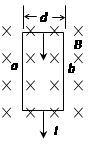
A．导体左侧聚集较多的电子
B．导体右侧聚集较多的电子
C．由于电子的聚集，使得左右两侧电势差为2Bdv
D．由于电子的聚集，使得左右两侧电势差为Bdv

参考答案：BD

本题解析：根据左手定则可知，电子受向右的电场力，所以导体右侧聚集较多的电子，故A错误B正确
当电子所受电场力和洛伦兹力平衡时，左右两端电势差恒定，即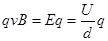，所以可得左右两侧电势差为Bdv，故C错误D正确
故选BD

本题难度：一般

4、计算题  如图所示，水平放置的导体框架，宽L＝0.5 m，接有电阻R＝0.3Ω，整个装置处于垂直框架平面向下的匀强磁场中，磁感应强度B＝0.4 T．一导体棒ab垂直框边跨放在框架上，并能无摩擦地在框架上滑动，已知导体棒ab的电阻为，框架的电阻均不计．当ab以v＝5.0 m/s的速度向右匀速滑动时，求：

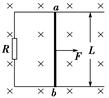
(1)ab棒中产生的感应电流的大小和方向；
(2)维持导体棒ab做匀速运动的外力F的大小；

参考答案：（1）b到a?2.0(A)（2）=0.4N

本题解析：(1)ab棒中的电流方向为b到a?（2分）
ab棒产生的感应电动势大小为E=BLV=1.0V?（2分）
ab棒中的电流大小为I="E/(R+r)" =2.0(A)? (2分)
（2）根据公式可得：F=F安=BIL=0.4N? (3分)
点评：本题是电磁感应与电路、力学知识的综合，安培力是联系力与电磁感应的桥梁，

本题难度：一般

5、选择题  穿过一个单匝线圈的磁通量始终为每秒均匀地增加2Wb，则（　　）
A．线圈中的感应电动势每秒增加2V
B．线圈中的感应电动势每秒减小2V
C．线圈中的感应电动势始终为2V
D．线圈中不产生感应电动势

参考答案：磁通量始终保持每秒钟均匀地增加2Wb，则磁通量的变化率为△?△t=2Wb1s=2V，
根据法拉第电磁感应定律E=n△?△t 可知E=2V保持不变．故C正确，A、B、D错误．
故选：C．

本题解析：

本题难度：简单