1、选择题  万有引力常数是由下列哪位科学家在实验室测量出来的（）
A．牛顿
B．杨振宁
C．卡文迪许
D．爱因斯坦

参考答案：C

本题解析：牛顿在推出万有引力定律的同时，并没能得出引力常量G的具体值．G的数值于1789年由卡文迪许利用他所发明的扭秤得出．卡文迪许的扭秤试验，不仅以实践证明了万有引力定律，同时也让此定律有了更广泛的使用价值．
解：顿在推出万有引力定律的同时，并没能得出引力常量G的具体值．G的数值于1789年由卡文迪许利用他所发明的扭秤得出．

故选C．

本题难度：简单

2、简答题  如图所示，2011年9月29日21时16分“天宫一号”从甘肃酒泉卫星发射中心发射升空，经过两次轨道控制，天宫一号已从入轨时的椭圆轨道进入在轨测试的近圆轨道，为后续与“神舟八号”交会对接奠定了基础．若天宫一号的测试轨道为r1，绕地球做匀速圆周运动的速度为v1；又已知某卫星绕地球做匀速圆周运动的速度为v2，轨道半径为r2，万有引力常量为G．根据以上信息，写出以下物理量的表达式：
（1）天宫一号的向心加速度；
（2）天宫一号”与卫星在各自轨道上运行的周期之比；
（3）地球的质量．

参考答案：（1）根据向心加速度公式a=v2r，有：
天宫一号的向心加速度a向=v12r12；
（2）周期等于旋转一周所用的时间，故：
天宫一号与卫星在各自轨道上运行的周期之比为T1T2=2πr1v12πr2v2=r1v2r2v1；
（3）天宫一号做匀速圆周运动的向心力有万有引力提供，有：GMmr12=mv12r1(或GMmr22=mv22r2)
解得：M=v12r1?G(或M=v22r2?G)
答：（1）天宫一号的向心加速度为v12r12；
（2）天宫一号与卫星在各自轨道上运行的周期之比为r1v2r2v1；
（3）地球的质量为v12r1?G(或v22r2?G)．

本题解析：

本题难度：一般

3、简答题  
（1）已知地球半径为R，地球表面重力加速度为g，地球自转周期为T0，请用以上物理量表示“风云二号”D气象卫星的轨道半径r，加速度a 以及线速度v ；
（2）取R=6400km，g=10m/s2，π2=10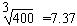，，求出“风云二号”D气象卫星的轨道半径r；
（3）根据第（2）问的结果，定性说明“风云二号”D气象卫星的加速度与随地球一块转动的赤道上物体的加速度的大小关系。

参考答案：
(1) 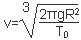?(2) 4.25×104km
(3)风云二号”D卫星的加速度大于赤道上随地球一块自转的物体的向心加速度

本题解析：（1）由题意知，“风云二号”D气象卫星为地球同步静止卫星，其运行周期和地球自转周期相等为T0，由万有引力提供向心力有方程式：
?
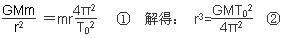又对地球表面的物体m"，地球对它的万有引力与重力相等：
?得：GM=gR2③

（2）将题中数据代入④式得：
?
=4.25×104km?（4分）
（3）“风云二号”D卫星与赤道上随地球一块自转的物体同做圆周运动，且有一样的周期，由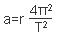知，T相同时，r越大，则a越大，通过第（2）问的计算结果表明r>R，则“风云二号”D卫星的加速度大于赤道上随地球一块自转的物体的向心加速度。（3分）
注意：只说明大小关系，但没有给出理由，只得1分

本题难度：简单

4、选择题  两颗行星A和B各有一颗卫星a和b，卫星轨道接近各自的行星表面，如果两行星质量之比为MA/MB=p，两行星半径之比RA/RB=q，则两卫星周期之比Ta/Tb为（?）
A．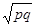
B．
C．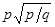
D．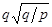

参考答案：D

本题解析：由周期公式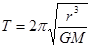，所以周期之比为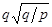

本题难度：简单

5、选择题  已知某行星绕太阳做匀速圆周运动的半径为r，公转周期为T，万有引力常量为G，下列说法正确的是（　　）
A．可求出行星的质量
B．可求出太阳的质量
C．可求出行星的绕行速度
D．可求出太阳的密度

参考答案：A、根据万有引力提供向心力，列出等式只能求出中心体的质量．故A错误
? B、研究卫星绕太阳做匀速圆周运动，根据万有引力提供向心力，列出等式mr4π2T2?=GMmr2可得太阳的质量．故B正确；
? C、行星的绕 行速度v=r2πT．故C正确
? D、不知道太阳的体积，所以不能求出太阳的密度．故D错误．
故选BC．

本题解析：

本题难度：简单