1、选择题 做匀变速直线运动的物体,它的加速度为a,在时间t内的位移为x,末速度为v,则此物体运动规律的表达式为?
[? ]
A.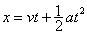
B. 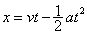
C. 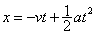
D.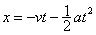
参考答案:B
本题解析:
本题难度:简单
2、计算题 (10分)如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验。若砝码和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ,重力加速度为g。
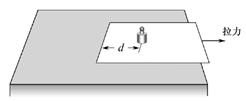
(1)当纸板相对砝码运动时,求纸板所受摩擦力的大小;
(2)要使纸板相对砝码运动,求所需拉力的大小;
(3)本实验中,m1 =0.5kg,m2 =0.1kg,μ=0.2,砝码与纸板左端的距离d=0.1m,取g ="10" m/ s2。若砝码移动的距离超过l ="0.002" m,人眼就能感知。为确保实验成功,纸板所需的拉力至少多大?
参考答案:(1) 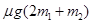 (2)F>
(2)F> (3)F=22.4N
(3)F=22.4N
本题解析:
 (1)砝码对纸板的摩擦力为
(1)砝码对纸板的摩擦力为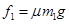 ,桌面对纸板的摩擦力
,桌面对纸板的摩擦力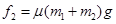 如图所示,
如图所示,
所以纸板受到的摩擦力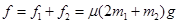
(2)设砝码的加速度为 ,由牛顿第二定律
,由牛顿第二定律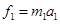
纸板的加速度为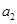 ,由牛顿第二定律
,由牛顿第二定律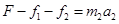
两物体发生相对运动,则 解得
解得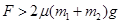
(3)纸板抽出前,砝码运动的距离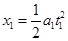
纸板运动的距离为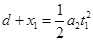
纸板抽出前,砝码在桌面上运动的距离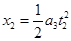
由物体的位移关系知砝码移动的距离超过l=x1+x2
由题意知,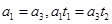
解得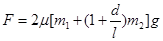
将m1 =0.5kg,m2 =0.1kg,μ=0.2,砝码与纸板左端的距离d=0.1m代入上式得F=22.4N
本题难度:一般
3、简答题 某一长直的赛道上有一辆赛车,其前方△x=200m处有一安全车正以v0=10m/s的速度匀速前进,这时赛车从静止出发以a=2m/s2的加速度追赶.试求:
(1)赛车出发3s末的瞬时速度大小?
(2)赛车经过多长时间追上安全车?
(3)赛车追上安全车之前,从开始运动起经过多长时间与安全车相距最远?
(4)赛车追上安全车之前与安全车最远相距是多少米?
(5)当赛车刚追上安全车时,赛车手立即刹车,使赛车以4m/s2的加速度做匀减速直线运动,问两车再经过多长时间第二次相遇?(设赛车可以从安全车旁经过而不发生碰撞)
参考答案:(1)由vt=v0+at,赛车出发3s末的瞬时速度大小:
v3=at
∴v3=6m/s
故3s末的瞬时速度大小为6m/s.
(2)设赛车经过时间t追上安全车,则有:
12at2-△x=v0t
∴t=20s
故经过20s赛车追上安全车.
(3)当两车速度相等时相距最远,对赛车:
v0=at′
∴t′=5s
故经过5s两车相距最远.
(4)当两车相距最远时,
赛车位移:x赛=12at/2
安全车位移:x安=v0t′
两车之间距离△x′=x安+△x-x赛
∴△x′=225m
故两车相距的最远距离为225m.
(5)第一次相遇时赛车的速度v20=at20=40m/s
设从第一次相遇起再经过时间T两车再次相遇,则:
v20T+12a/T2=v0T
∴T=30s
但赛车速度从40m/s减为零只需10s,
所以两车再次相遇的时间:0-v2202a/=v0T/
∴T′=20s
故经过20s两车再次相遇.
本题解析:
本题难度:一般
4、简答题 汽车以5m/s的速度在水平路面上匀速前进,紧急制动后在粗糙水平面上滑行的加速度大小为2m/s2,求:刹车后3s内汽车通过的位移.
参考答案:汽车做匀减速运动经时间t速度减为零,由匀变速运动规律得:
0=v0-at?①
代入解得t=2.5s<3s故3s时汽车早已停止运动?②
故物体运动的位移为x:x=v0+02t?③
解得:x=6.25m?④
答:刹车后3s内汽车通过的位移为6.25m.
本题解析:
本题难度:一般
5、计算题 (12分)甲物体从某高楼离地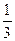 楼高处自由下落,最后1s通过的位移是全程的
楼高处自由下落,最后1s通过的位移是全程的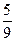 ,令甲物体下落同时,从楼顶竖直向下抛乙物体(有一定的初速度,加速度为g),两物体恰好同时落地,不计空气阻力,g取10m/s2,求:
,令甲物体下落同时,从楼顶竖直向下抛乙物体(有一定的初速度,加速度为g),两物体恰好同时落地,不计空气阻力,g取10m/s2,求:
(1)竖直下抛的乙物体的初速度;
(2)甲、乙两物体着地时的速度.
参考答案:(1)30m/s?(2)30 m/s? 60 m/s
本题解析:(1)设甲物体运动的总时间为t,楼高为h,则在甲物体下落的整个过程中以及前(t-1)s内应用自由落体运动位移公式,有
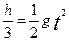 ? ---------(2分)
? ---------(2分)
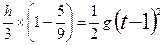 ? ---------(2分)
? ---------(2分)
解得: t=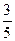 s(不合题意,舍去),t="3s?" ---------(1分)
s(不合题意,舍去),t="3s?" ---------(1分)
h="135m?" ---------(1分)
设乙物体以初速度v0下抛,则由匀变速直线运动位移公式,有
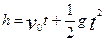 ?
?
解得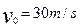 ?---------(2分)
?---------(2分)
(2)由速度公式,可得甲、乙物体着地时的速度分别为
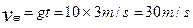 ,? ---------(2分)
,? ---------(2分)
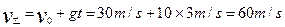 ? ---------(2分)
? ---------(2分)
本题难度:简单
Against the assault of laughter nothing can stand. 无人能抵御嘲笑的进攻。