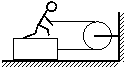
1、填空题  如图所示，人重600N，木块重400N，人与木块、木块与水平面间的动摩擦因数为0.2，不计绳、滑轮的重力及绳与滑轮间的摩擦，现在人用水平力拉绳，使它与木块一起向右作加速度a=1m/s2的匀加速直线运动，则人拉绳的力是______N，人受的摩擦力大小为______N，方向______．

参考答案：
由人重600N，木块重400N，可知人的质量M=60kg，木块的质量m=40kg
对人和木块整体受力分析知其受绳的拉力，摩擦力，由牛顿第二定律得：
2F-μ（M+m）g=（M+m）a
2F-0.2×1000=100×1
解得：F=150N
对人受力分析，其受绳的拉力，摩擦力，由牛顿第二定律：
F-f=Ma
150-f=60×1
解得：f=90N
方向水平向左
故答案为：150；90；水平向左

本题解析：

本题难度：一般

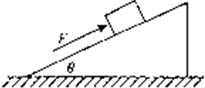
2、简答题  质量为m=3kg的木块放在倾角为θ=30°的足够长斜面上，木块可以沿斜面匀速下滑．若用沿斜面向上的力F作用于木块上，使其由静止开始沿斜面向上加速运动，经过t=2s时间物体沿斜面上升4m的距离来源:91考试网 91Exam.org，求力F的大小？（g取10m/s2）

参考答案：物体匀速下滑时，受重力，摩擦力，支持力，沿斜面方向可得：
f=mgsinθ；
已知物块由静止开始沿斜面向上加速运动，经过t=2s时间物体沿斜面上升4m的距离，由位移时间关系可得：
s=12at2，
解得：
a=2st2=2×422m/s2=2m/s2
对物块受力分析，可知其受重力，推力，摩擦力，支持力．
沿斜面方向：
F-mgsinθ-f=ma
解得：
F=2mgsinθ+ma=2×3×10×12N+3×2N=36N；
答：力F的大小为36N．

本题解析：

本题难度：一般

3、简答题  如图甲为消防员训练时的一种器械，一质量不计的竖直滑竿，滑竿上端固定，下端悬空．为了研究消防员沿竿的下滑情况，在竿的顶部装有一拉力传感器，可显示竿的顶端所受拉力的大小．现有一质量m=50kg的消防员（可视为质点）从滑竿顶端由静止开始滑下，4s末滑到竿A点时开始匀速下滑．以消防员开始下滑时刻为计时起点，传感器显示的拉力随时间变化情况如图乙所示，g取10m/s2．求：
（1）该消防员下滑过程中的最大速度．
（2）A点到滑竿顶端的长度．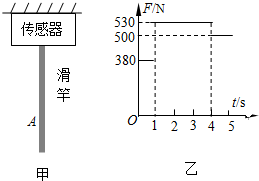

参考答案：（1）由题意分析知：传感器显示的拉力大小为消防员所受竿的摩擦力的大小．
由F-t?知：消防员先加速下滑1s末开始减速下滑，4s末后匀速下滑，所以最大速度出现在1s末：
?0～1s，由牛顿第二定律：F合=ma?
所以：mg-f=ma1
即：500-380=50a1；得a1=2.4m/s2．
?1s末的速度：v1=at=2.4×1m/s=2.4m/s．
（2）0～1s的位移：s1=12at2=12×2.4×12=1.2m
?1～4s的加速度：
a2=F合m=mg-fm=500-53050=-0.6m/s2．
?1～4的位移：
s2=v0t+12at2=2.4×3+12×(-0.6)×32=4.5m
?A点到滑杆顶端的长度：
h=s1+s2=1.2+4.5m=5.7m．
答：（1）该消防员下滑过程中的最大速度为2.4m/s．
（2）A点到滑竿顶端的长度为5.7m．

本题解析：

本题难度：一般

4、简答题  如图所示，倾角为θ的斜面上静止放置三个质量均为m的木箱，相邻两木箱的距离均为l．工人用沿斜面的力推最下面的木箱使之上滑，逐一与其它木箱碰撞．每次碰撞后木箱都粘在一起运动．整个过程中工人的推力不变，最后恰好能推着三个木箱匀速上滑．已知木箱与斜面间的动摩擦因数为μ，重力加速度为g．设碰撞时间极短，求
（1）工人的推力；
（2）三个木箱匀速运动的速度；
（3）在第一次碰撞中损失的机械能．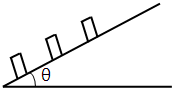

参考答案：（1）当匀速时，把三个物体看作一个整体受重力、推力F、摩擦力f和支持力．
根据平衡的知识有
F=3mgsinθ+3μmgcosθ．
（2）第一个木箱与第二个木箱碰撞之前的速度为V1，加速度a1=F-mgsinθ-μmgcosθm=2g（sinθ+μcosθ）
根据运动学公式或动能定理有V1=2

本题解析：

本题难度：一般

5、简答题  如图所示是一传送带加速装置示意图，现利用该装置，将一货物轻放在速度足够大的传送带A端，将其加速到另一端B后货物将沿着半径R=0.4m的光滑半圆轨道运动，半圆轨道与传送带在B点相切，其中BD为半圆轨道的直径，O点为半圆轨道的圆心．已知传送带与货物间的动摩擦因数μ=0.8，传送带与水平面间夹角θ=37°．已知sin37°=0.6，cos37°=0.8，g取10m/s2，货物可视为质点．求：
（1）货物在传送带上的加速度大小；
（2）若货物能沿半圆轨道运动到最高点C，传送带AB段至少要多长？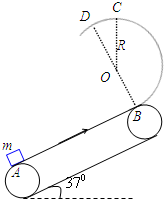

参考答案：（1）物体在沿AB加速过程中，由牛顿第二定律得：
μmgcosθ-mgsinθ=ma，解得：a=0.4m/s2；
（2）要使小球能沿轨道刚好到达最高点C，
重力提供圆周运动的向心力，在C点，
由牛顿第二定律得：mg=mv2CR，
解得：vC=

本题解析：

本题难度：一般