1、计算题  （11分）甲、乙两车在同一条平直公路上运动，甲车以10 m/s 的速度匀速行驶，经过车站A时关闭油门以4m/s2的加速度匀减速前进，2s后乙车与甲车同方向以1m/s2的加速度从同一车站A出发，由静止开始做匀加速运动，问乙车出发后多少时间追上甲车？

2、选择题  某同学根据自己的生活体验设置了这样一个问题：甲物体沿直线MN做匀速直线运动，速度为v1. P点到MN的垂直距离为s，如图所示. 乙物体由P点开始运动，要追上甲物体. 设乙物体可沿任意方向运动且速度大小始终是v2. 已知v2>v1. 某时刻当甲位于直线MN上的F点时，乙物体由P点开始运动，问，乙物体能否追上甲物体？哪种追赶方式用时最短？同学们通过分析以后得出以下几种不同的观点，你认为正确的是（?）

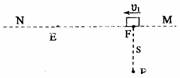
A．乙物体沿PFN的路线追赶甲物体时，用时最短
B．乙物体追赶过程中，保持其速度的方向总是指向甲物体，这样运动方式用时最短
C．通过计算，使乙物体沿某直线PE运动，到达直线MN时正好与甲物体相遇，这种方式用时最短
D．在A、B、C三种追赶方式中，乙物体都能追上甲物体

3、选择题  A、B、C三物体同时同地出发做直线运动，它们的运动情况如图所示，在20 s时间内，下列说法不正确的是（?）

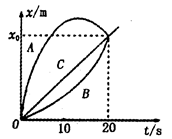
A．三者路程相等
B．三者位移相等
C．B物体一直加速到达x0处
D．C物体一直匀速到达x0处

4、计算题  如图所示是做直线运动的物体M在0～5 s的x－t图象，求：
（1）前3 s的平均速度大小；
（2）全程的平均速度大小；
（3）最后1 s的速度大小；
（4）画出其V-t图象。

5、计算题  羚羊从静止开始奔跑，经过50m能加速到最大速度25m/s并能维持这个速度较长的时间。猎豹从静止开始奔跑，经过60m能达到最大速度30m/s，以后只能维持这个速度4s。设猎豹与羚羊x米时开始攻击，羚羊在猎豹开始攻击后1s 才开始奔跑。设它们在加速阶段均作匀加速直线运动，求：
小题1:猎豹要在最大速度减速前追上羚羊，求x的范围。
小题2:猎豹要在加速阶段追上羚羊。求x的范围。