1、选择题  质子（p）和α粒子以相同的速率在同一匀强磁场中作匀速圆周运动，轨道半径分别?为?RP?和?R，周期分别为?TP?和?T，则下列选项正确的是（　　）
A．R：Rp=2：1；T：Tp=2：1
B．R：Rp=1：1；T：Tp=1：1
C．R：Rp=1：1；T：Tp=2：1
D．R：Rp=2：1；T：Tp=1：1

参考答案：质子（11P）和α粒子（42He）以相同的速度垂直进入同一匀强磁场中，均做匀速圆周运动．
则由轨迹的半径为：R=mvBq得：半径与这两粒子的质量与电量的比值成正比．即R：Rp=2：1
而周期公式：T=2πmBq得：周期与这两粒子的质量与电量的比值成正比．即T：Tp=2：1
故选A

本题解析：

本题难度：简单

2、简答题  如图所示，在y轴右方有一垂直纸面向里的匀强磁场，磁感应强度B=0.20T．有一质子以速度v=2.0×106m/s，从x轴上的A点（10cm，0）沿与x轴正方向成30°斜向上射入磁场．质子质量取m=1.6×10-27kg，电量q=1.6×10-19C，质子重力不计．求：
（1）质子在磁场中做圆周运动的半径；
（2）质子在磁场中运动所经历的时间．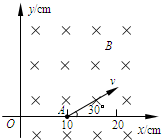

参考答案：

（1）质子在磁场中受洛仑兹力做匀速圆周运动，
根据牛顿第二定律得qvB=mv2R
质子做匀速圆周运动的半径为：R=mvqB=0.10m
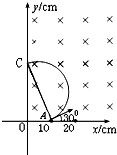
（2）由于质子的初速度方向与x轴正方向的夹角为30°，且半径恰好等于0.10m，
因此质子将在磁场中做半个圆周运动到达y轴上的C点，如图所示．
根据圆周运动的规律，质子做圆周运动的周期?为：T=2πmqB
质子从出发到第一次到达y轴所经历的时间为：t=T2=πmqB≈1.57×10-7s
答：（1）质子在磁场中做圆周运动的半径0.1m；
（2）质子在磁场中运动所经历的时间1.57×10-7s．

本题解析：

本题难度：一般

3、简答题  一光滑圆柱体，固定在地面上，现用长为圆柱体的

参考答案：（1）根据共点力平衡，有T=GA sin 37°
T=GB sin 53°
所以GA?sin?37°=GB?sin?53°，
则GB=GA?tan?37°=6?N，
（2）取整根绳子为研究对象，受到两个小球的拉力和圆柱面的弹力作用，三力平衡，
T=GA?sin?37°=4.8?N，
所以N=

本题解析：

本题难度：一般

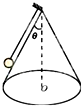
4、填空题  长为l的细线上端固定在顶角为74°的固定光滑圆锥体的顶部，下端与质量为m的小球（可看做质点）相连，如图．让小球绕圆锥体的中心以角速度ω在水平面内做匀速圆周运动．（已知sin37°=0.6；cos37°=0.8）
（1）当ω2=______时，圆锥体对小球的支持力恰好为0；
（2）当ω2=

参考答案：（1）小球刚要离开锥面时的速度，此时支持力为零，根据牛顿第二定律得：
mgtanθ=mω02lsinθ
解得：ω02=5g4l，
（2）当ω2=

本题解析：

本题难度：简单

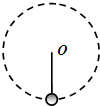
5、选择题  如图所示，长为L的细绳，一端系一质量为m的小球，另一端固定于O点．当细绳竖直时小球静止，再给小球一水平初速度v，使小球在竖直平面内做圆周运动，并且刚好通过最高点，则下列说法中正确的是（　　）
A．小球通过最高点时速度为零
B．小球开始运动时绳对小球的拉力为m