1、选择题  在距地面15 m高处，某人将一质量为4 kg的物体以5 m/s的速度抛出，人对物体做的功是
[? ]
A、20 J
B、50 J
C、588 J
D、638 J

参考答案：B

本题解析：

本题难度：简单

2、简答题  如图所示，质量为m，带电量为+q的微粒在0点以初速度v0与水平方向成θ?角射出，微粒在运动中受阻力大小恒定为f．
①如果在某方向加上一定大小的匀强电场后，能保证微粒仍沿u方向做直线运动，试求所加匀强电场的最小值？
②若加上大小一定，方向水平向左的匀强电场，仍能保证微粒沿vo方向做直线运动，并经过一段时间后又返回o点，求微粒回到o点时的速率？

参考答案：（

1）微粒受力如图所示，要保证微粒沿vo方向直线运动必须使垂直于vo方向斜上方加匀强电场，E有最小值，且Eq=mgcosθ，E=mgcosθq．
（2）如图所示，为使垂直于v0方向合力为零，Eqsinθ=mgcosθ．设微粒最大位移为S，由动能定理
-（mgsinθ+qEcosθ+f）S=0-12mv20
粒子由O点射出再回到O点整个过程，由动能定理
-2fS=12mv2-12mv20．
解上述方程得
v=

本题解析：

本题难度：一般

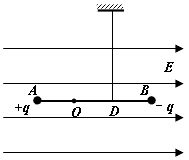
3、计算题  如图所示，绝缘轻杆长L＝0.9m，两端分别固定着带等量异种电荷的小球A、B，质量分别为mA＝4×10-2kg，mB＝8×10-2kg，A球带正电，B球带负电，电荷量q＝6.0×10-6C。轻杆可绕过O点的光滑水平轴转动，OB＝2OA。一根竖直细线系于杆上OB中点D使杆保持水平，整个装置处在水平向右的匀强电场中，电场强度E＝5×104N/C。不计一切阻力，取g＝10m/s2，求：
（1）细线对杆的拉力大小；
（2）若将细线烧断，当轻杆转过90°时，A、B两小球电势能总的变化量；
（3）细线烧断后，在杆转动过程中小球A的最大速度。

参考答案：解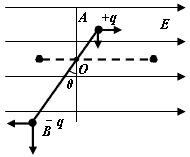：（1）根据有固定转动轴物体的平衡条件，有

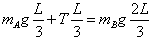
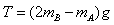＝（2×8×10-2－4×10-2）×10＝1.2N
（2）杆转过90°时，电场力对两带电小球做正功，电势能减少
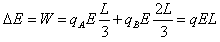＝6.0×10-6×5×104×0.9＝0.27J
（3）当力矩的代数和为零时，B球的速度达到最大

＝
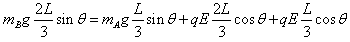
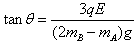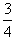
θ＝37°
由动能定理：

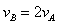
联立求得：vA＝2m/s

本题解析：

本题难度：困难

4、计算题  分）如图所示，空间存在着强度E=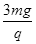方向竖直向上的匀强电场，在电场内一长为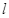的绝缘细线，一端固定在O点，一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求：

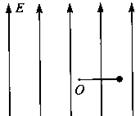
（1）小球运动最高点时的速度；
（2）细线能承受的最大拉力；
（3）从断线开始计时，在t=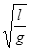时刻小球与O点的距离。

参考答案：（1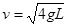）；（2）6mg；（3）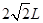

本题解析：
试题分析:
（1）设小球运动到最高点时速度为v，只有重力和电场力做功，弹力不做功。对该过程由动能定理有，
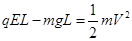?①?（2分）
解得?（1分）
（2）在最高点，小球受三个力作用，重力，电场力和细线的拉力，由向心力公式得，
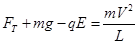?②（2分）
解得，T=6mg（1分）
（2）小球在细线断裂后，带电小球做类平抛运动，合力竖直向上的，在竖直方向的加速度设为a，则
?③（2分）
小球在t时刻
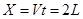?（1分）
?（1分）
小球与O点的距离
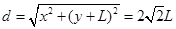? (2分）

本题难度：一般

5、选择题  世界男子网坛现年排名第一的瑞士选手费德勒，在上海大师杯网球赛上发出一记S球，声纳测速仪测得其落地速度为V1，费德勒击球时球离地面的高度为h，击球瞬间球有竖直向下的速度V0，已知网球质量为m，不计空气阻力，则费德勒击球时对球做的功W为（?）
A．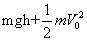
B．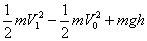
C．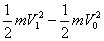
D．

参考答案：D

本题解析：根据动能定理，将发球直至球落地整个过程分析得 ，可见D正确。

本题难度：简单