1、简答题 如图所示,劲度系数为k的轻弹簧,右端连在竖直墙面上,左端连着不带电的绝缘小球B,开始时B球静止在光滑绝缘水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现把一质量为m、带电荷量为+q的小球A,从距B球s处自由释放,A将与B发生正碰.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球的质量M=2m,B球被碰后作简谐运动,其运动周期T=2π
(A、B小球均可视为质点).求:
(1)A球与B球第一次相碰前A的速度大小;
(2)两球第一次碰后瞬间,A球的速度v1和B球的速度v2;
(3)要使A球与B球第二次仍在B球的初始位置相碰,弹簧劲度系数k的可能取值.
参考答案:(1)设A球与B球第一次碰撞前瞬间的速度为v0,由动能定理得:
? qE?s=12mv2
解得:v0=
本题解析:
本题难度:一般
2、简答题 如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带电量为q的粒子从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.(忽略粒子重力)求:
(1)该带电粒子从e孔射出的速度大小.
(2)该过程中电场力对该带电粒子做的功.
(3)若正方形的边长为l,试求该电场的场强.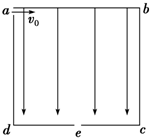
参考答案:
本题解析:
本题难度:一般
3、选择题 一个质量为1kg的物体被人用手由静止开始向上提升1m,这时物体的速度为2m/s,则下列结论中正确的是:
[? ]
A.手对物体做功12J
B.合力对物体做功12J
C.合力对物体做功2J
D.物体克服重力做功10J
参考答案:ACD
本题解析:
本题难度:一般
4、计算题 如图所示,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与R=0.24m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以v0=6m/s的初速度滑上小车左端,二者共速时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2,求:
(1)滑块与小车共速时的速度及小车的最小长度;
(2)滑块m恰好从Q点离开圆弧轨道时小车的长度;
(3)讨论小车的长度L在什么范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道?
参考答案:(1)L1="3m(2)" 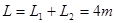 (3) (3)
本题解析:(1)由动量守恒知,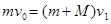 , ,
得v1=4m/s(4分)设小车的最小长度为L1
由能量守恒知 ,得L1=3m(4分) ,得L1=3m(4分)
(2)m恰能滑过圆弧的最高点,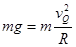 (2分) (2分)
小车粘在墙壁后,滑块在车上滑动,运动到最高点Q,
在这个过程对滑块由动能定理: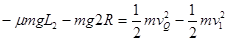 (2分) (2分)
解得: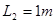
所以小车长度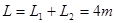 (2分) (2分)
(3)由(2)可知,滑块要想运动到Q点,小车的长度L必须满足: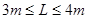
若滑块恰好滑至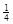 圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道。 圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道。
小车粘在墙壁后,滑块在车上滑动,运动到T点, 在这个过程对滑块由动能定理: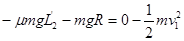 (2分) (2分)
解得 (2分) (2分)
本题考查的是动量守恒和动能定理的应用。
本题难度:一般
5、选择题 下列叙述中正确的是
[? ]
A.合外力对物体做功为零的过程中,物体的机械能一定守恒
B.物体在合外力作用下做变速运动,则物体动能一定变化
C.物体的动能不变,则物体所受的合外力一定为零
D.当只有重力或弹簧弹力对物体做功时,物体和地球或弹簧系统的机械能一定守恒
参考答案:D
本题解析:
本题难度:简单
One never goes to the temple for no reason. 无事不登三宝殿。 |