1、计算题  如图所示，放在水平面上质量为m=0.4kg的物体，在水平力F1=3N的作用下作匀速直线运动，现在若再对物体施加一个力F，且F与F1在同一竖直面内，要使物体仍作匀速直线运动，则F与F1的夹角θ为多大？

参考答案：解：物体在水平力F1的作用下作匀速直线运动，物体受到四个力作用：重力mg、弹力N1、拉力F1、滑动摩擦力f1，且这四个力的合力为零。现再加一个外力F后，物体仍做匀速直线运动，说明物体所受合力仍然为零，因注意到此时弹力、滑动摩擦力都发生了变化，不再是原来的值，都变小了，设为N2与f2，而动摩擦因数μ未变，物体的两次受力图如图所示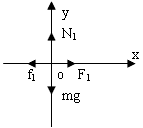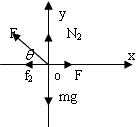：? 根据平衡条件第一次：，，，
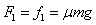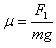
第二次：，，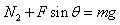
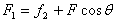
由此可得：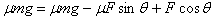
，θ=53°
F与F1的夹角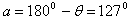

本题解析：

本题难度：困难

2、简答题  物体速度为零，一定处于平衡状态吗？

参考答案：速度为零时，物体不一定处于平衡状态。如将物体竖直上抛运动到最高点时，v=0，a=g。必须同时满足F合=0（或a=0）才能说平衡状态。

本题解析：

本题难度：一般

3、选择题 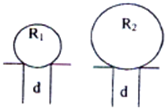 宽度同为d的水平光滑直角槽，槽两边在同一水平面，上面分别放两个质量分布均匀的小球，两个球的质量相同，半径为R1和R2，每个球受到槽单侧边沿的弹力分别为FN1和FN2，己知R2＞R1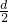＞，则FN1和FN2的关系正确的是
A.FN1=FN2
B.FN1＜FN2
C.FN1＞FN2
D.以上条件不能确定FN1和FN2的大小关系

参考答案：C

本题解析：分析：分析小球的受力情况，由平衡条件得出小球受到的槽单侧边沿的弹力大小与两弹力夹角之间的关系．根据数学知识得出两弹力夹角的大小关系，再判断FN1和FN2的关系．
解答：解：设任意一球受到槽单侧边沿的两个弹力之间的夹角为2α，弹力大小为FN，小球的重力大小为G．由平衡条件可知，两个弹力FN的合力大小等于G，方向与G相反．
根据平衡条件得：2FNcosα=G，得FN=
己知R2＞R1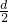＞，由几何知识得知，两个FN2之间的夹角较小，cosα较大，FN较小，即有：FN1＞FN2
故选C
点评：此题运用平衡条件和几何知识结合进行分析，也可以根据合力与分力的关系：两个分力大小一定，夹角越大，合力越小进行判断．

本题难度：一般

4、计算题  (10分）如图所示，AB、BC均为轻细杆，处在同一竖直平面内，AB杆高为h=0.8m。A、B、C三处均用铰接连接，其中A、C两点在同一水平面上，BC杆与水平面夹角为30°。一个质量为m=2kg的小球（可视为质点）穿在BC杆上，对小球施加一个水平向左的恒力F使小球静止在BC杆中点处，不计一切摩擦。(g取10m/s2)，求：

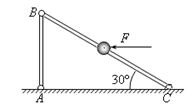
（1）恒力F的大小；
（2）此时AB杆对B处铰链的作用力大小和方向。

参考答案：（1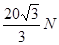）（2）

本题解析：（1）由受力平衡可知

(2)建立直角坐标系可得
?（5分）
点评：本题难度较小，对于此类问题首先明确研究对象，对于受力较多的情况采用正交分解法

本题难度：一般

5、选择题 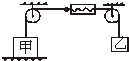 如图所示，甲物重5N，乙物重3N．甲、乙均静止，不计弹簧测力计自重，则弹簧测力计示数是
A.3N
B.5N
C.2N
D.0N

参考答案：A

本题解析：分析：弹簧测力计示数显示弹簧秤受到的拉力大小．对乙研究，由平衡条件得到弹簧秤的拉力．
解答：对乙：处于静止状态，受力平衡，则有弹簧秤的拉力大小为F=G乙=3N，所以弹簧测力计示数是3N．
故选A
点评：本题要注意弹簧测力计示数显示弹簧秤受到的拉力大小，不是受到的合力大小，以弹簧秤一侧的物体作为研究对象求解．

本题难度：困难