1、选择题 如图质量为m的小球,从离桌面高H处由静止下落,桌面离地面高为h,设桌面处物体重力势能为零,空气阻力不计,那么,小球落地时的机械能为(?)

A.mgh
B.mgH
C.mg(H+h)
D.mg(H-h)
参考答案:B
本题解析:在整个过程中,小球的机械能守恒,设桌面处物体重力势能为零,则子刚开始下落时球的动能为零,重力势能为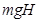 ,所以此时的机械能即为
,所以此时的机械能即为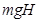 ,故小球落地时的机械能也为
,故小球落地时的机械能也为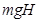 .
.
故选B.
点评:全过程中球的机械能都守恒,只要求得其中一点的机械能就可以知道机械能的大小.
本题难度:一般
2、选择题 如图甲所示,一轻弹簧的两端与质量分别为m1和m2的两物块A、B相连接,并静止在光滑的水平面上.现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得( )
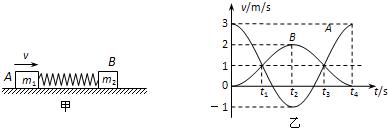
A.在t1、t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态
B.从t3到t4时刻弹簧由压缩状态恢复到原长
C.两物体的质量之比为m1:m2=1:2
D.在t2时刻A与B的动能之比为Ek1:Ek2=1:8
参考答案:A、由图可知t1、t3时刻两物块达到共同速度1m/s,且此时系统动能最小,根据系统机械能守恒可知,此时弹性势能最大,弹簧处于压缩状态,故A正确;
B、结合图象弄清两物块的运动过程,开始时m1逐渐减速,m2逐渐加速,弹簧被压缩,t1时刻二者速度相当,系统动能最小,势能最大,弹簧被压缩最厉害,然后弹簧逐渐恢复原长,m2依然加速,m1先减速为零,然后反向加速,t2时刻,弹簧恢复原长状态,由于此时两物块速度相反,因此弹簧的长度将逐渐增大,两木块均减速,当t3时刻,二木块速度相等,系统动能最小,弹簧最长,因此从t3到t4过程中弹簧由伸长状态恢复原长,故B错误;
C、系统动量守恒,选择开始到t1时刻列方程可知:m1v1=(m1+m2)v2,将v1=3m/s,v2=1m/s代入得:m1:m2=1:2,故C正确;
D、在t2时刻A的速度为:vA=1m/s,B的速度为:vB=2m/s,根据m1:m2=1:2,求出Ek1:Ek2=1:8,故D正确.
故选ACD.
本题解析:
本题难度:简单
3、简答题 如图所示,物块A的质量为M,物块B、C的质量都是m,并都可看作质点,且m<M<2m。三物块用细线通过滑轮连接,物块B与物块C的距离和物块C到地面的距离都是L。现将物块A下方的细线剪断,若物块A距滑轮足够远且不计一切阻力。求:

小题1:物块A上升时的最大速度;
小题2:?物块A上升的最大高度。
参考答案:
小题1: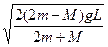
小题2:H3 ?= ?2L+ h’ = 2L +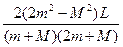 ??
??
本题解析:
小题1:A、B、C三物体系统机械能守恒。B、C下降L,A上升L时,A的速度达到最大。? 2mgL-MgL=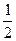 (M+2m)V2? 2分? V=
(M+2m)V2? 2分? V=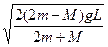 ??
??
小题2:当C着地后,A、B二物体系统机械能守恒。B恰能着地,即B物体下降L时速度为零。? MgL-mgL =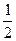 (M+m)V2?
(M+m)V2?
将V代入,整理后得:M=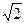 m?
m?
若M>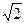 m,B物体将不会着地。
m,B物体将不会着地。
Mgh-mgh =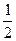 (M+m)V2?
(M+m)V2?
h =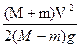 ?
?
HL = L + h = L +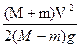 ?
?
若M =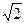 m,B恰能着地,A物体再上升的高度等于L。H2 = 2L?
m,B恰能着地,A物体再上升的高度等于L。H2 = 2L?
若M<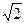 m,B物体着地后,A还会上升一段。
m,B物体着地后,A还会上升一段。
Mg L-mg L =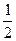 (M+m)(V2-v2)?
(M+m)(V2-v2)?
V2 =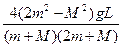 ?
?
h’=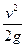 =
=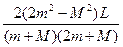 ?
?
H3 ?= ?2L+ h’ = 2L +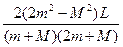 ??
??
本题难度:一般
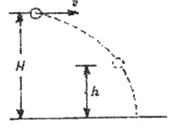
4、选择题 如图所示,从H高处以v平抛一小球,不计空气阻力,当小球距地面高度为h时,其动能恰好等于其势能,则(取地面为参考平面)
A.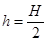
B.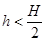
C.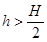
D.无法确定
参考答案:C
本题解析:
试卷分析:根据机械能守恒定律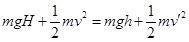 ,且
,且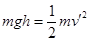 ,因此
,因此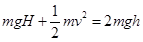 ,即
,即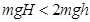 ,所以C答案正确。
,所以C答案正确。
点评:此类题型考察机械能守恒定律,并根据题目意思并结合不等式求解。
本题难度:简单
5、选择题 如图所示,用长为L的绳子一端系着一个质量为m的小球,另一端固定在O点,拉小球至A点,此时绳子偏离竖直方向为θ角,空气阻力不计,松手后小球经过最低点的速率为

[? ]
A.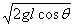
B.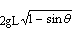
C.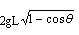
D.2gL
参考答案:C
本题解析:
本题难度:一般