1、选择题  如图为质点受某恒力做曲线运动的轨迹示意图，且质点运动到D点时速度方向与加速度方向恰好互相垂直，则质点从A点运动到E点的过程中，下列说法中正确的是(　　)

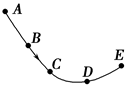
A．质点经过C点的速率比D点的大
B．质点经过A点时的加速度方向与速度方向的夹角小于90°
C．质点经过D点时的加速度比B点的大
D．质点从B到E的过程中加速度方向与速度方向的夹角先增大后减小

参考答案：A

本题解析：物体做曲线运动的条件是合力与速度不在同一条直线上，速度的方向与该点曲线的切线方向相同；由牛顿第二定律可以判断加速度的方向．
A、质点做匀变速曲线运动，由动能定理可得，D点的速度比C点速度大，故A正确；
B、质点运动到D点时速度方向与加速度方向恰好互相垂直，则有A、B、C三点速度与加速度方向夹角大于90°，故B错误；
C、质点做匀变速曲线运动，则有加速度不变，所以质点经过D点时的加速度与B点相同，故C错误；
D、质点从B到E的过程中加速度方向与速度方向的夹角减小，故D错误；
故选：A。
点评：本题关键是对质点做曲线运动的条件的考查，掌握了做曲线运动的条件，本题基本上就可以解决了．

本题难度：简单

2、选择题  物体受几个外力作用下恰好做匀速直线运动，如果突然撤去其中的一个力F，其他力不变，则它可能做
A．匀速直线运动
B．匀加速直线运动　　　
C．静止
D．曲线运动

参考答案：BD

本题解析：撤去其中一个力后，其他力的合力与F的关系是等大反向，所以物体做匀变速运动，当合力与速度共线时为直线运动，反之为曲线运动，BD对；

本题难度：简单

3、选择题  如图所示，质量为m的物块与转台之间能出现的最大静摩擦力为物体重力的k倍，它与转轴OO/相距R，物块随转台由静止开始转动。当转速增加到一定值时，物块即将在转台上滑动。在物块由静止到开始滑动前的这一过程中，转台对物块做的功为

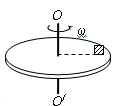
A．0
B．2πkmgR
C．2kmgR
D．kmgR/2

参考答案：D

本题解析：分析：通过题目情境我们发现在物块由静止到开始滑动前的这一过程中，转台对物块的作用力是一个变力，
对于变力做的功我们应该首先想到运用动能定理．
对于圆周运动的临界问题，我们要通过临界条件列出等式．
解答：解：由于物体做圆周运动，物体刚开始滑动这一时刻，物体受到转台的摩擦力达到最大静摩擦力去提供向心力．
即：kmg=m，v2=kgR．
设转台对物块做的功为W转，运用动能定理研究在物块由静止到开始滑动前的这一过程，
W转=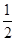mv2-0=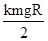
故选D．

本题难度：简单

4、选择题  关于曲线运动，下列说法中正确的是
A．做曲线运动的物体其速度大小一定变化
B．做曲线运动的物体加速度方向一定变化
C．做匀速圆周运动的物体，所受合外力不一定时刻指向圆心
D．平抛运动是一种匀变速曲线运动

参考答案：D

本题解析：曲线运动中，只是速度方向时刻发生变化，大小有可能不变，例如匀速圆周运动，选项A错误；做曲线运动的物体加速度方向可能不变，例如平抛运动，选项B错误；做匀速圆周运动的物体，所受合外力一定时刻指向圆心，选项C错误；平抛运动中物体加速度保持恒定不变，为匀变速曲线运动，选项D正确；故选BD
点评：本题难度较小，曲线运动分为匀变速曲线运动和变加速曲线运动

本题难度：一般

5、选择题  如图所示。宇航员站在某星球表面一斜坡上P点沿水平方向以初速度V抛出一个小球。测得小球经时间t落到斜面上另一点Q。斜面的倾角为θ已知该星球半径为R，求：

⑴该星球表面的重力加速度？⑵该星球的第一宇宙速度？

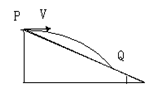
参考答案：?, V=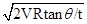

本题解析：（1）小球做平抛运动，水平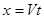位移，竖直位移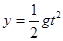，由位移关系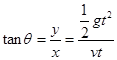得：，解得，
（2）该星球的近地卫星的向心力由万有引力提供
该星球表面物体所受重力等于万有引力，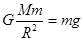
联立解得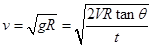

本题难度：简单