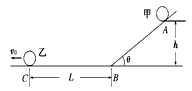
1、计算题  如图所示，小球甲从倾角θ＝30°的光滑斜面上高h＝5cm的A点由静止释放，同时小球乙自C点以速度v0沿光滑水平面向左匀速运动，C点与斜面底端B处的距离L＝0.4m．甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去，甲释放后经过t＝1s刚好追上乙，求乙的速度v0。

2、简答题  如图所示，一质量为M=4kg，长为L=1.5m的木板放在水平地面上，已知木板与地面间动摩擦因数为0.1，在此木板的右端上还有一质量为m=1kg的铁块，且视小铁块为质点，木板厚度不计；今对木板突然施加一个水平向右的拉力．?
①若不计铁块与木板间的摩擦，且拉力为8N，则小铁块经多长时间将离开木板？
②若铁块与木板间的动摩擦因数为0.2，铁块与地面间的动摩擦因数为0.1，要想小铁块对地的总位移不超过1.5m，则施加在木板水平向右的拉力满足什么条件？（g=10m/s2）

3、计算题  以10m/s的速度匀速行驶的汽车，刹车后做匀减速直线运动。若汽车刹车后第2s内的位移为6.25m（刹车时间超过2s），则刹车后6s内汽车的位移是多大？

4、计算题  计算下列物体的加速度：
(1)汽车启动时，从静止开始做匀加速直线运动，经10s速度达到72km/h；
(2)沿光滑水平地面以12m/s运动的小球,撞墙后以原来速度大小反弹回来,与墙壁接触时间为0.2s。

5、选择题  两物体从同一地点同时出发，沿同一方向做匀加速直线运动，若它们的初速度大小不同，而加速度大小相同，则在运动过程中（?）
A．两物体速度之差保持不变
B．两物体的速度之比与时间成正比
C．两物体的位移之差与时间成正比
D．两物体的位移之差与时间的平方成正比