1、计算题 (18分)如图a所示,竖直直线MN左方有水平向右的匀强电场,现将一重力不计,比荷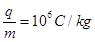 的正电荷置于电场中O点由静止释放,经过
的正电荷置于电场中O点由静止释放,经过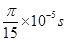 后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求:
后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求:
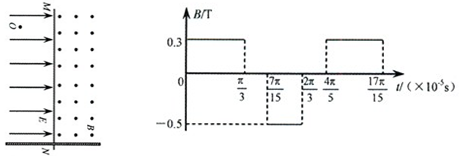
(1)匀强电场的电场强度E;
(2)图b中 时刻电荷与O点的竖直距离r。
时刻电荷与O点的竖直距离r。
(3)如图在O点下方d=39.5cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需要的时间。(结果保留2位有效数字)
参 考答案:7.2×103N/C? 4cm? 2.1×10-4s
本题解析:(1)电荷在电场中做匀加速直线运动,设其在电场中运动的时间为t1 ,有:
根据
解得: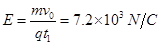
(2)当磁场垂直纸面向外时,电荷运动的半径: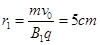
周期
当磁场垂直纸面向里时,电荷的运动半径: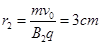 周期:
周期: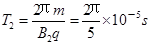
电荷从t=0进入磁场开始做周期性运动,其运动轨迹如图所示

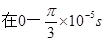 时间内,带电粒子经时间
时间内,带电粒子经时间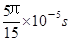 完成半周期圆周运动进入电场,在电场中往返时间为
完成半周期圆周运动进入电场,在电场中往返时间为 ,再次进入磁场,磁场方向发生变化,经
,再次进入磁场,磁场方向发生变化,经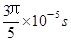 完成半周期圆周运动,再次进入电场,在电场中往返时间为
完成半周期圆周运动,再次进入电场,在电场中往返时间为 ,距O点的距离为4cm.
,距O点的距离为4cm.
(3)电荷从第一次通过MN开始,其运动的周期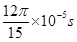 ,
,
根据电荷的运动情况,可知,电荷到达挡板前运动的完整周期数为8个,此时电荷沿MN运动的距离: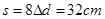 ?
?
则最后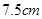 的距离如图乙所示,
的距离如图乙所示,

有: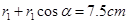
解得: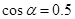 ,则
,则 ? (3分)
? (3分)
故电荷运动的总时间
 ? (3分)
? (3分)
本题难度:一般
2、计算题 如图所示,在直角坐标系xOy平面内有一矩形区域MNPQ,矩形区域内有水平向右的匀强电场,场强为E;在y 0的区域内有垂直于坐标平面向里的匀强磁场,半径为R的光滑绝缘空心半圆管ADO固定在坐标平面内,半圆管的一半处于电场中,圆心O1为MN的中点,直径AO垂直于水平虚线MN,一质量为m、电荷量为q的带电粒子(重力不计)从半圆管的O点由静止释放,进入管内后从A点穿出恰能在磁场中做半径为R的匀速圆周运动,当粒子再次进入矩形区域MNPQ时立即撤去磁场,此后粒子恰好从QP的中点C离开电场。求
0的区域内有垂直于坐标平面向里的匀强磁场,半径为R的光滑绝缘空心半圆管ADO固定在坐标平面内,半圆管的一半处于电场中,圆心O1为MN的中点,直径AO垂直于水平虚线MN,一质量为m、电荷量为q的带电粒子(重力不计)从半圆管的O点由静止释放,进入管内后从A点穿出恰能在磁场中做半径为R的匀速圆周运动,当粒子再次进入矩形区域MNPQ时立即撤去磁场,此后粒子恰好从QP的中点C离开电场。求
(1)匀强磁场的磁感应强度B的大小;
(2)矩形区域的长度MN和宽度MQ应满足的条件?
(3)粒子从A点运动到C点的时间。

参考答案:解:(1)粒子从O到A过程中由动能定理得 ?
?
从A点穿出后做匀速圆周运动,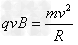
解得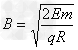 ?
?
(2)粒子再次进入矩形区域后做类平抛运动,由题意得


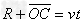
联立解得
所以,矩形区域的长度MN 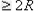 ,宽度MQ
,宽度MQ 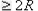
(3)粒子从A点到矩形边界MN的过程中,
从矩形边界MN到C点的过程中,
故所求时间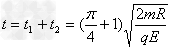
本题解析:
本题难度:一般
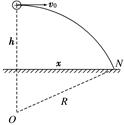
3、计算题 (11分)如图10所示,一质量为m、电荷量为q的带正电的小球以水平初速度v0从离地高为h的地方做平抛运动,落地点为N,不计空气阻力,求:

(1)若在空间加一个竖直方向的匀强电场,使小球沿水平方向做匀速
直线运动,则场强E为多大?
(2)若在空间再加上一个垂直于纸面向外的匀强磁场,小球的落地点仍?
为N,则磁感应强度B为多大?
参考答案:(1)  (2)
(2) 
本题解析:(1)由于小球受电场力和重力且做匀速直线运动,故qE=mg,所以E= .
.
(2)再加上匀强磁场后,由于重力与电场力平衡,故小球在洛伦兹力作用下做匀速圆周
运动R=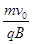
由几何关系得:
R2-x2=(R-h)2
其中x=v0t=v0
由以上几式解得:B= .
.
本题难度:一般
4、选择题 如图表示水平方向的匀强磁场和竖直方向的匀强电场叠加区域,一个质量是m带电量是q的质点B恰好能静止在区域中间,另一个质量为2m,带电量也为q的质点A恰好能以某一速度沿着垂直于磁场、电场方向做匀速直线运动,且正好与静止的质点B发生正碰,碰后两质点粘在一起运动,碰撞的过程无电量损失,则下列正确的是
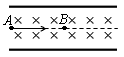
[? ]
A.碰后两质点的运动向下偏且动能增加
B.碰后两质点的运动向上偏且动能增加
C.碰后两质点的运动向上偏且动能减少
D.碰后两质点的运动向下偏且动能减少
参考答案:C
本题解析:
本题难度:一般
5、计算题 在如图所示xoy坐标系第一象限的三角形区域(坐标如图中所标注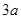 和
和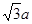 )内有垂直于纸面向外的匀强磁场,在x 轴下方有沿+y方向的匀强电场,电场强度为E。将一个质量为m、带电量为+q的粒子(重力不计)从P(0,-a)点由静止释放。由于x轴上存在一种特殊物质,使粒子每经过一次x轴后(无论向上和向下)速度大小均变为穿过前的
)内有垂直于纸面向外的匀强磁场,在x 轴下方有沿+y方向的匀强电场,电场强度为E。将一个质量为m、带电量为+q的粒子(重力不计)从P(0,-a)点由静止释放。由于x轴上存在一种特殊物质,使粒子每经过一次x轴后(无论向上和向下)速度大小均变为穿过前的 倍。
倍。
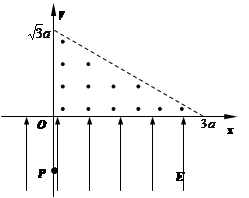
(1)欲使粒子能够再次经过x轴,磁场的磁感应强度B0最小是多少?
(2)在磁感应强度等于第(1)问中B0的情况下,求粒子在磁场中的运动时间。
参考答案:(1)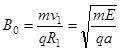 (2)
(2)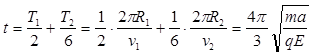
本题解析:解:⑴设粒子到O点时的速度为v0,
由动能定理有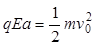 ?(2分)
?(2分)
解得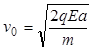 ?(2分)
?(2分)
粒子经过O点后,速度为v1,
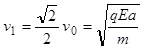 ?(2分)
?(2分)
如图所示,粒子进入磁场后的轨迹圆与磁场边界相切时,磁感应强度最小为B0。

设粒子轨道半径为R1,有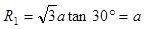 ?(2分)
?(2分)
由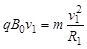 得?
得?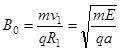 ?(2分)
?(2分)
⑵如图,粒子经O1点进入电场区域做匀减速运动,后又加速返回,再次进入磁场时的速率
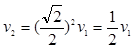 ?(1分)
?(1分)
此时粒子做圆周运动的半径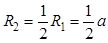 ?(1分)
?(1分)
其运动轨迹如图甲所示,此后不再进入磁场。由几何关系可知,
 ?(2分)
?(2分)
粒子在磁场中运动的周期为: ?(2分)
?(2分)
则粒子在磁场中运动的时间为: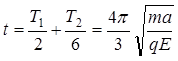 ?(2分)
?(2分)
或: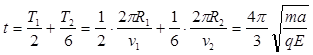 (4分)
(4分)
本题考查的是带电粒子在匀强电场和匀强磁场的复合场中的运动问题。分析清楚带电粒子在匀强电场和匀强磁场的复合场中的运动情况,应用带电粒子在匀强电场和匀强磁场的规律进行计算。
本题难度:一般