1、简答题  如图所示，质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上，质量为2m的小明同学站在小车上用力向右迅速推出木箱后，小明和小车获得的速度大小为v，木箱在与右侧竖直墙壁发生碰撞后，以等大反向的速度反弹回来，最后木箱又被小明接住，求小明接住木箱后三者共同速度的大小．

参考答案：取向左为正方向，根据动量守恒定律有：
推出木箱的过程，0=（m+2m）v-mv1
接住木箱的过程mv1+（m+2m）v=（m+m+2m）v2
解得共同速度为v2=1.5v．
答：小明接住木箱后三者的共同速度大小为1.5v．

本题解析：

本题难度：一般

2、简答题  如图5－10所示，倾角θ=30°，高为h的三角形木块B，静止放在一水平面上，另一滑块A，以初速度v0从B的底端开始沿斜面上滑，若B的质量为A的质量的2倍，当忽略一切摩擦的影响时，要使A能够滑过木块B的顶端，求V0应为多大？

参考答案：

本题解析：【错解分析】错解：设滑块A能滑到h高的最小初速度为v，滑块A到达斜面最高点时具有水平分速度为V′，由于水平方向不受外力，所以水平方向动量守恒，由动量守恒定律：
mv0cosθ=mv′＋Mv′ ①
　　在B的上端点m的合速度为：

　　由动能定理有：
　
　　
　　　
　　主要是对滑块A滑过最高点的临界状态分析不清楚。实际上，当滑块能够到达最高点时，即其竖直向上的分速度为零，也就是说，在最高点，滑块A只具有水平速度，而不具有竖直速度。所以，式①是正确的，式②中关于滑块A的动能，直接代入水平速度即可。
　　【正确解答】 根据水平方向动量守恒有：
mv0cosθ=(m+M)v′ ①
　　
　　
　　
　　【小结】 分析此题时，可以先定性分析，从题目可以知道，V0越大，上升的距离越高；v0较小，则可能上不到顶端。那么，刚好上升到
　　v0＞v时，才能够滑过。对于题目中的关键字眼，“滑过”、“至少”等要深入挖掘。

本题难度：一般

3、填空题  A、B两物体在光滑的水平面上发生碰撞，碰撞前后物体的运动都在同一条直线上。规定A物体原运动方向为正方向。A物体的质量。若不计碰撞时间，它们碰撞前后的位移图像如图所示。碰撞前B的质量为；碰撞过程中A物体的动量改变量是。

参考答案：1.5、? -1.5

本题解析：根据图象可知，碰前A的速度，B静止不动，碰后A、B速度相同，为，根据动量守恒定律，，整理得，；
A动量变化

本题难度：一般

4、简答题  最初斜面和木箱均静止，后来木箱自光滑斜面滑下，如图16-10所示，木箱和斜面的质量分别为m="10" kg和M="50" kg，斜面长L="2" m,不计斜面与地面的摩擦，斜面倾角为30°.求木箱滑至斜面底部时斜面移动的距离.

图16-10

参考答案：

本题解析：取木箱和斜面为一个系统研究，在水平方向上无外力作用，此系统的动量在水平方向上是守恒的.
设斜面后退的距离为x,则木箱移动的水平距离为Lcos30°-x,根据水平方向动量守恒知
M·x=m(Lcos30°-x),
整理得
.

本题难度：简单

5、简答题  如图所示，质量为0.4kg的木块以2m/s的速度水平地滑上静止的平板小车，车的质量为1.6kg，木块与小车之间的摩擦系数为0.2(g取10m/s2)。设小车足够长，求：
（1）木块和小车相对静止时小车的速度。
（2）从木块滑上小车到它们处于相对静止所经历的时间。
（3）从木块滑上小车到它们处于相对静止木块在小车上滑行的距离。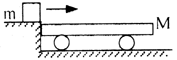

参考答案：（1）0.4m/s
（2）0.8s
（3）0.8m

本题解析：（1）以木块和小车为研究对象，系统所受合外力为零，系统动量守恒，以木块速度方向为正方向，由动量守恒定律可得：
木块m?小车M
初：v0="2m/s?" ?v0=0
末：v?v
即mv0=(M+m)v，
得。
（2）再以木块为研究对象，其受力情况如图所示，由动量定理可得：


。
（3）木块做匀减速运动，加速度，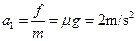
车做匀加速运动，加速度，由运动学公式可得：
vt2-v02=2as，
在此过程中木块的位移，
车的位移，
由此可知，木块在小车上滑行的距离为ΔS=S1-S2=0.8m，即为所求。
另解：设小车的位移为S2，则A的位移为S1+ΔS，ΔS为木块在小车上滑行的距离，那么小车、木块之间的位移差就是ΔS，作出木块、小车的v-t图线如图所示，则木块在小车上的滑行距离数值上等于图中阴影部分的三角形的“面积”。

本题难度：简单