1、简答题  半径为R的光滑半圆环形轨道固定在竖直平面内，从与半圆环相吻合的光滑斜轨上高h=3R处，先后释放A、B两小球，A球的质量为2m，B球的质量为m，当A球运动到圆环最高点时，B球恰好运动到圆环最低点，如图所示．求：
（1）此时A、B球的速度大小vA、vB；
（2）这时A、B两球对圆环作用力的合力大小和方向．

参考答案：（1）对A分析：从斜轨最高点到半圆环形轨道最高点，由机械能守恒得：
2mg（3R-2R）=12?2mv2A
解得：vA=

本题解析：

本题难度：一般

2、简答题  如图所示，在同一竖直平面内两正对着的相同半圆光滑轨道，轨道半径R=2m，相隔一定的距离x，虚线沿竖直方向，一质量M=0.1kg的小球能在其间运动．今在最低点B与最高点A各放一个压力传感器，测试小球对轨道的压力，并通过计算机显示出来．已知小球在最低点B的速度为vB=20m/s，取g=10m/s2，不计空气阻力．求：
（1）小球在最低点B对轨道的压力．
（2）小球能沿光滑轨道运动到最高点A时，x的最大值．
（3）若半圆轨道的间距x可在零到最大值之间变化，试在图中画出小球对轨道B、A两点的压力差随距离x变化的图象．

参考答案：
（1）小球在最低点时，根据牛顿第二定律得
? ?FB-Mg=Mv2MR
? 代入解得FB=21N?
?又根据牛顿第三定律：小球在最低点B对轨道的压力为21N．
（2）小球恰好到达最高点A时，
? Mg=Mv2AR? ?①
小球从A到B的过程，根据机械能守恒定律得
? Mg（2R+x）+12Mv2A=12Mv2B? ②
联立①②，代入解得? x=15m
（3）设小球对轨道B、A两点的压力大小分别为FB、FA．
以小球为研究对象，根据牛顿第二定律得


? A点：Mg+FA=Mv2AR? ③
? B点：FB-Mg=Mv2BR? ④
又Mg（2R+x）+12Mv2A=12Mv2B? ⑤
△FN=FB-FA ⑥
联立③④⑤⑥得
△FN=x+6?
作图象如图．?
答；
（1）小球在最低点B对轨道的压力为21N．
（2）小球能沿光滑轨道运动到最高点A时，x的最大值为15m．
（3）小球对轨道B、A两点的压力差随距离x变化的图象如图所示．

本题解析：

本题难度：一般

3、填空题  如图1所示，某汽车以不变的速率驶入一个狭长的

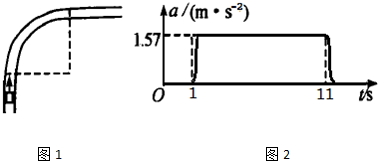
参考答案：从图象可知，有向心加速度的时间为10s，则汽车经过弯道时的时间为10s，则汽车做圆周运动的周期T=40s，根据a=r（2πT）2，知，r=aT24π2．
则转弯的速率v=2πrT=aT2π=1.57×403.14×2m/s=10m/s．
故答案为：10；10

本题解析：

本题难度：一般

4、选择题  如图所示，叠放在水平转台上的小物体A、B、C能随转台一起以角速度ω匀速转动，A、B、C的质量分别为3m、2m、m，A与B、B与转台、C与转台间的动摩擦因数都为μ，B、C离转台中心的距离分别为r、1.5r．设本题中的最大静摩擦力等于滑动摩擦力．以下说法中正确的是（　　）
A．B对A的摩擦力一定为3μmg
B．C与转台间的摩擦力大于A与B间的摩擦力
C．要使物体与转台不发生相对滑动，转台的角速度一定满足：ω≤

2μg 3r D．要使物体与转台不发生相对滑动，转台的角速度一定满足：ω≤ μg 3r 参考答案：A、对A受力分析，受重力、支持力以及B对A的静摩擦力，静摩擦力提供向心力，有f=（3m）ω2r≤μ（3m）g．故A错误． B、由于A与C转动的角速度相同，由摩擦力提供向心力有m×1.5rω2＜3mrω2即C与转台间的摩擦力小于A与B间的摩擦力，故B错误； C、对AB整体，有：（3m+2m）ω2r≤μ（3m+2m）g…① 对物体C，有：mω2（1.5r）≤μmg…② 对物体A，有：3mω2r≤μ（3m）g…③ 联立①②③解得：ω≤ 本题解析： 本题难度：简单 5、简答题  如图，带电量为+q、质量为m的粒子（不计重力）由静止开始经A、B间电场加速后，沿中心线匀速射入带电金属板C、D间，后粒子由小孔M沿径向射入一半径为R的绝缘筒，已知C、D间电压为U0，板间距离为d，C、D间与绝缘筒内均有垂直于纸面向里的匀强磁场，磁感应强度分别为B0、B． （1）求粒子在C、D间穿过时的速度v0； （2）求A、B间的加速电压U； （3）粒子与绝缘筒壁碰撞，速率、电荷量都不变，为使粒子在筒内能与筒壁碰撞4次（不含从M孔出来的一次）后又从M孔飞出，求筒内磁感应强度B?（用三角函数表示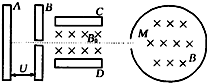）． 参考答案：（1）∵粒子在C、D间做匀速运动，则： Eq=B0qv0?而E=U0d?有：粒子在C、D间的速度v0=U0dB0 （2）粒子在A、B间加速过程有：qU=12mv20?在C、D间匀速运动有：qE=qv0B0 且E=U0/d?解得：U=mU202qB20d2 （3）带电离子在圆形磁场中运动的可能轨迹如图： 由（1）得：v0=U0B0d 离子在圆形磁场中有：qv0B=mv20r． 所以B=mv0qr=mU0B0dqr 如图所示：r=Rtanθ2由几何知识易知：5θ=2nπ，n=1或2? 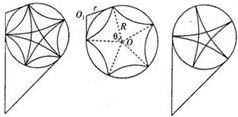第一种情况：θ=2π5，则r=Rtanπ5，所以B=mU0B0dqr=mU0qB0dRtan(π5) 第二种情况：θ′=4π5， 则r′=Rtan2π5，B=muoqB0dRtan(2π5) 答：（1）粒子的速度为V0=U0dB0 （2）A、B间的加速电压为U=?mU022qB02d2 （3）可能的运动轨迹如图所示，对应的B为mu0qB0dRtan(π5)或mU0qB0dRtan(2π5)． 本题解析： 本题难度：一般