1、简答题  用图示装置做“研究有固定转动轴物体平衡条件”的实验，力矩盘上各同心圆的间距相等．在用细线悬挂钩码前，已经采取的措施有：
①检查力矩盘是否处在竖直平面．
还必须采取的检查措施有
②______
③______．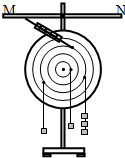

参考答案：本实验沿验证力矩平衡条件，故要使力矩盘的重心处于转轴位置，要尽量减小力矩盘与转轴间摩擦力的影响；
故答案为：判断力矩盘与转轴间的摩擦是否足够小，判断力矩盘的重心是否位于盘中心．

本题解析：

本题难度：一般

2、简答题  某种汽车的制造标准是车身在横向倾斜300角时不翻倒，如图所示。若车轮间距离为2m，那么车身重心G离斜面的高度应不超过多少米？

参考答案：h = 1.73m。

本题解析：以车为研究对象，进行受力分析

只要重力的作用线不超过车轮的支持面，车就不会翻倒。车轮与斜面的接触点A是支持面的接触边缘。在直角三角形AGO中，∠AGO = 300，AO = = 1m，则重心高h = = m = 1.73m。

本题难度：一般

3、简答题  如图所示，OAB是一刚性轻质直角三角形支架，边长AB=0.2m，∠OAB=37°；在A、B两顶角处各固定一个大小不计的小球，质量均为1kg．支架可绕过O的水平轴在竖直平面内无摩擦地转动．（sin37°=0.6，cos37°=0.8，重力加速度g取10m/s2）
（1）为使支架静止时AB边水平，求在支架上施加的最小力；
（2）若将支架从AB位于水平位置开始由静止释放，求支架转动过程中A处小球速度的最大值．

参考答案：（1）施加的最小力满足的条件是：力臂最大
所以该力的作用在A点，方向垂直于OA向上，根据力矩平衡条件，有：
mg?OA?cos37°=mg?OB?cos53°+Fmin?OA
OA=0.16m，OB=0.12m，可解得：Fmin=3.5N
作用在A点，在支架平面内垂直于OA向上
（2）支架力矩平衡时两小球的速度最大．
设平衡时OA边与竖直方向夹角为θ
则有mg?OA?sinθ=mg?OB?sin（90°-θ），可得θ=37°
根据系统机械能守恒定律，有：
mg（OAcos37°-OAcos53°）-mg（OBcos37°-OBcos53°）=12m（v12+v22）
其中v1：v2=OA：OB=4：3
由上述两式可解得：v1=0.32m/s
答：（1）在支架上施加的最小力为3.5N，作用于A点且垂直AC边向上；
（2）支架转动过程中A处小球速度的最大值为0.32m/s．

本题解析：

本题难度：一般

4、选择题  如图所示，轻质支架ABC中，AB和AC用光滑铰链在A处连接，AC垂直于地面，B、C分别用光滑铰链铰在水平面上，今沿着AB杆方向作用于AB一个斜向上的拉力F，AB与AC成45°角，两杆均处于静止状态，则AC杆在A处受到的作用力大小为（　　）
A．F
B.
C.
D．0