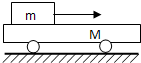
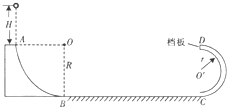
1、简答题  如图所示，AB和CD处于竖直平面内的光滑圆弧轨道，OA处于水平位置．AB是半径为R=2m的

2、计算题  (11分) 如右图所示的电路中，两平行金属板A、B水平放置，两板间的距离d="40" cm.电路电压恒为U=24V，电阻R=16Ω。闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度v0="4" m/s竖直向上射入板间。若小球带电荷量为q=1×10-2 C，质量为m=2×10-2 kg，不考虑空气阻力。

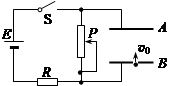
求：（1）滑动变阻器接入电路的阻值为多大时，小球恰能到达A板？
（2）此时滑动变阻器消耗功率是多大？(取g="10" m/s2)

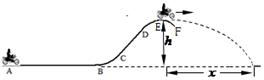
3、计算题  运动员驾驶摩托车做腾跃特技表演。如图所示，AB是水平路面，长度为L=100m，BCD是一段曲面，AB、BC相切于B点， DEF是一段半径为R=10m的圆弧曲面，E为圆弧的顶点。运动员驾驶摩托车的功率恒定。从A点由静止出发，经过t1=15s到B点，在AB段所受的阻力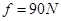，摩托车过B点时速度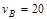m/s，再经t2=2s的时间，摩托车通过圆弧曲面的顶点E，此时压力传感器显示摩托车对E点的压力为零，摩托车通过E后做平抛运动，落地点与E点的水平距离为x＝18m。已知人车总质量为m=180kg，重力加速度g＝10m/s2。求：

小题1:摩托车在AB段的最小加速度a
小题2:坡顶高度h
小题3:人和摩托车在BE段克服空气和摩擦阻力做的功W

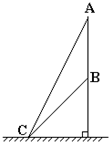
4、选择题  如图所示，质量相同的物体分别自斜面AC和BC的顶端由静止开始下滑，物体与斜面间的动摩擦因数都相同，物体滑到斜面底部C点时的动能分别为Ek1和Ek2，下滑过程中克服摩擦力所做的功分别为W1和W2，则（　　）
A．Ek1＞Ek2　W1＜W2
B．Ek1＞Ek2　W1=W2
C．Ek1=Ek2　W1＞W2
D．Ek1＜Ek2　W1＞W2