|
高中物理知识点大全《向心力与向心加速度》试题特训(2019年最新版)(八)
2019-07-03 00:32:26
【 大 中 小】
|
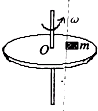
1、选择题 如图所示,小物块m与圆盘保持相对静止,并随圆盘一起做匀速圆周运动,则小物块?的受力情况是( )
A.受重力、支持力、静摩擦力和向心力的作用
B.摩擦力的方向始终与小物体运动方向相反
C.重力和支持力是一对相互作用力
D.摩擦力是使物体做匀速圆周运动的向心力
| 
参考答案:A、小物块受重力、支持力、和静摩擦力作用,靠静摩擦力提供向心力,静摩擦力的方向指向圆心.故A错误,B错误,D正确.
C、重力和支持力是一对平衡力.故C错误.
故选D.
本题解析:
本题难度:简单
2、计算题 如图所示,在光滑的圆锥顶用长为l的细线悬挂一质量为m的小球,圆锥体固定在水平面上不动,其轴线沿竖直方向,母线与轴线之间的夹角30°,物体以角速度ω绕圆锥体轴线做水平匀速圆周运动。试求:
(1)当ω 时,绳对物体的拉力; 时,绳对物体的拉力;
(2)当ω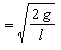 时,绳对物体的拉力。 时,绳对物体的拉力。
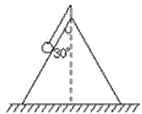
参考答案:解:当小球和圆锥体之间弹力刚好为0时,设此时物体旋转角速度为ω0,此时对物体受力分析如图,有:?  ? ? 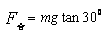
? 
? 由得 ,得 ,得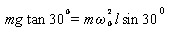 ? ?
? 
(1)当ω 时,ω< 时,ω< ,此时小球与圆锥体斜面有弹力作用,设为N,对小球受力分析: ? ,此时小球与圆锥体斜面有弹力作用,设为N,对小球受力分析: ?  ? ? 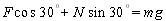 ?① ?①
? 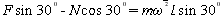 ?② ?②
? 由①②得: ,方向与竖直方向成30°夹角向上 ,方向与竖直方向成30°夹角向上
(2)当ω 时,ω> 时,ω>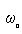 ,对小球受力分析:? ,对小球受力分析:? 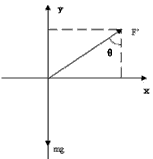 ? ? 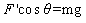 ?③ ?③
?  ?④ ?④
? 由③④得: , ,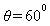 ? ?
? 此时绳对物体拉力大小为2mg,方向与竖直方向成60°夹角向上
本题解析:
本题难度:困难
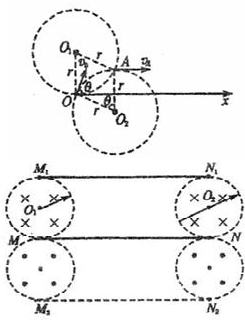
3、简答题 真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,ox为磁场边界上的切线,如图所示.从o点在纸面内向各个方向发射速率均为v0的带负电的粒子,设带电粒子间相互作用可忽略,且此种带负电的粒子在磁场中的偏转半径也是r.
(1)所有从磁场边界射出的带负电的粒子,速度方向有何特征?请通过几何关系来说明此种带负电粒子的速度方向特征.
(2)速度方向分别与ox轴正方向成60°与90°的带负电粒子,在磁场中的运动时间分别是多少?
(3)已知电子的质量为m,电量为e.今在某一平面内有M、N两点,MN=l,从M点向平面内各个方向发射速率均为v0的电子,请在图中设计一个匀强磁场分布,使得由M点发出的电子都能够汇聚到N点(要求在图中画出磁场的范围),并求出匀强磁场的磁感应强度B的最小值.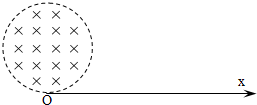
参考答案:(1)如图所示,入射时电子速度与x夹角为θ,无论入射的速度方向与x轴的夹角为何值,由入射点O、射出点A、磁场圆心O1和轨道圆心O2一定组成边长r的菱形,因O1O⊥OX,OO2垂直于入射速度,故∠OO2A=θ,即电子在磁场中所偏转的角度一定等于入射时电子速度与Ox轴的夹角.
当θ=60°时,t1=π6=πr3v
当θ=90°时,t2=π4=πr2v
(2)因∠OO2A=θ,故O1A⊥OX,而O2A与电子射出的速度方向垂直,可知电子射出方向一定与Ox轴方向平行,即所有的电子射出圆形磁场时,速度方向均与Ox轴相同.
(3)上述的粒子路径是可逆的,(2)中从圆形磁场射出的这些速度相同的电子再进入一相同的匀强磁场后,一定会聚集于同一点.磁场的分布如图所示,对于从M点向MN连线上方运动的电子,两磁场分别与MN相切,M、N为切点,且平行于两磁场边界圆心的连线O1O2.
设MN间的距离为l,所加的磁场的边界所对应圆的半径r,故应有2r≤l,即2mveB≤l,所以所加磁场磁感应强度应满足B≥2mvel.
同理,对于从M点向MN连线下方运动的电子,只要使半径相同的两圆形磁场与上方的两圆形磁场位置关于MN对称且磁场方向与之相反即可说明:只要在矩形区域M1N1N2M2内除图中4个半圆形磁场外无其他磁场,矩形M1N1N2M2区域外的磁场均可向其余区域扩展.
本题解析:
本题难度:一般
4、填空题 如右图所示,圆弧轨道AB是在竖直平面内的 圆周,在B点轨道的切线是水平的,一质点自A点从静止开始下滑,滑到B点时的速度大小是 圆周,在B点轨道的切线是水平的,一质点自A点从静止开始下滑,滑到B点时的速度大小是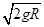 ,重力加速度为g,则在质点刚要到达B点时的加速度大小为__________,滑过B点时的加速度大小为____________. ,重力加速度为g,则在质点刚要到达B点时的加速度大小为__________,滑过B点时的加速度大小为____________. 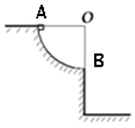
参考答案:2g? g
本题解析:质点从A到B做的是圆周运动,在B点的加速度等于向心加速度,大小为 ;滑过B点后质点做平抛运动,只受重力,加速度为g。 ;滑过B点后质点做平抛运动,只受重力,加速度为g。
点评:本题难点是判断质点的运动状态,到达B点前是圆周运动,加速度为向心加速度,过了B点就不是圆周运动了,根据以后的运动规律判断加速度。
本题难度:简单
5、简答题 如图所示,有一可绕竖直中心轴转动的水平圆盘,上面放置劲度系数为k的弹簧,弹簧的一端固定于轴O上,另一端连接质量为m的小物块A(可视为质点),物块与圆盘间的动摩擦因数为μ,开始时弹簧未发生形变,长度为L0,若最大静摩擦力与滑动摩擦力大小相等,重力加速度为g,物块A始终与圆盘一起转动.则:
(1)圆盘的角速度多大时,物块A将开始滑动?
(2)当圆盘角速度缓慢地增加到4 时,弹簧的伸长量是多少?(弹簧伸长在弹性限度内且物块未脱离圆盘)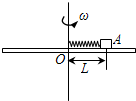
参考答案:(1)设盘的角速度为ω0时,物块A将开始滑动,则
μmg=mRω02时?
解得?ω0=
本题解析:
本题难度:一般
|
|
