1、简答题 (1)在探究“弹簧的弹力和伸长量的关系”的实验中,某同学根据实验数据作出了弹力F和弹簧伸长量x的关系图象,如图1F-x?图象,有图象数据可知,次弹簧的劲度系数k=______N/m.
(2)在“探究求合力的方法”实验中,通过实验探究出两个力合成的法则.
即:______定则.按照此定则得到的合力的作用效果与原来两个力的作用效果是______的(填“相同”或“不同”),若互相垂直的两个力的大小分别为3N和4N,则合力大小为______N.
(3)在探究“加速度与力、质量的关系”的实验中,采用了______,即:保持______不变时,探究加速度与力的关系;保持______不变时,探究加速度与质量的关系.
实验采用了如图2所示装置,图中用软木塞将木板一端适当垫高,是为了______.
通过同学们的实验探究,并相互交流,总结出加速度与力、质量的关系是:______,______.
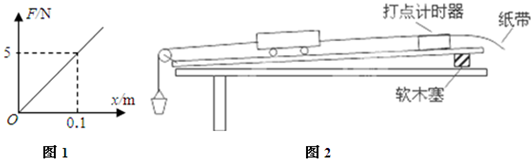
参考答案:(1)F-x图象斜率大小等于弹簧的劲度系数,由图象可知,弹簧劲度系数k=Fx=50.1=50N/m.
(2)两个力合成的法则是平行四边形定则;合力的作用效果与原来两个力的作用效果是相同;
互相垂直的两个力的大小分别为3N和4N,则合力F=
本题解析:
本题难度:一般
2、填空题 一轻质弹簧原长10cm,甲乙两人同时用100N的力在两端反向拉弹簧,其长度变为12cm,若将弹簧一端固定,由甲一人用100N的力拉,则此时弹簧长度为 cm,此弹簧的劲度系数为 N/m。
参考答案:12 cm 5000n/m
本题解析:甲乙两人同时用100N的力在两端反向拉弹簧和将弹簧一端固定,由甲一人用100N的力拉,弹簧的伸长量相等,所以x=12cm,根据胡克定律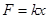 可得
可得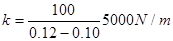
考点:考查了胡克定律的应用
点评:公式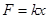 中的x表示弹簧的形变量
中的x表示弹簧的形变量
本题难度:一般
3、实验题 在探究“弹簧的弹力与伸长的关系”实验中,通过在悬挂的弹簧下面加挂钩码,逐渐使弹簧伸长,得到以下的数据.
由数据在坐标中画出图象.
由此得到结论:?.
弹簧的劲度系数k =?N / m.(取两位有效数字)
钩码个数
| 1
| 2
| 3
| 4
| 5
| 6
|
弹簧弹力F(N)
| 0.50
| 1.00
| 1.50
| 2.00
| 2.50
| 3.00
|
弹簧伸长x(cm)
| 1.20
| 2.40
| 3.60
| 4.76
| 6.10
| 7.10
|
?
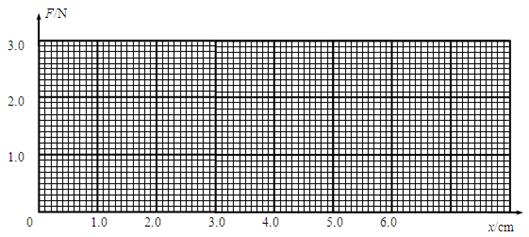
参考答案:(1)弹簧的弹力与伸长成正比
(2)42或43

本题解析:略
本题难度:简单
4、简答题 以下是一位同学在做“探究形变与弹力的关系”的实验中.为了探究弹力大小与弹簧伸长量之间的关系所测的几组数据如表:
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5
弹簧原来长度(L0/cm)
15
15
15
15
15
弹簧后来长度(L/cm)
16.2
17.3
18.5
19.6
20.8
弹簧伸长量(x/cm)
1.2
2.3
3.5
4.6
5.8
|
①根据上表的数据在图的坐标中作出F-x图线.
②写出曲线的函数表达式.(x用cm作单位):______
③函数表达式中常数的物理意义:______.
参考答案:①图线如图所示.
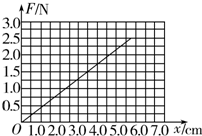
②根据图象,该直线为过原点的一条直线,即弹力与伸长量成正比,图象的斜率表示弹簧的劲度系数
k=△F△x=2.5N5.70×10-2m≈438.6N/m
故函数表达式为:F=438.6x
③图线的物理意义是表示弹力与伸长量成正比,其中438.6为斜率,表示劲度系数;
故答案为:①如图所示;②F=438.6x;③劲度系数.
本题解析:
本题难度:一般
5、实验题 实验题(19分):
(1)某同学用螺旋测微器测量某一导线的直径,测量结果如下图甲所示,则该导线的直径为???mm.该同学再用主尺最小分度为1mm,游标上有20个分度的卡尺测量某金属球的直径,测量结果如下图乙所示,则该金属球的直径为?cm.
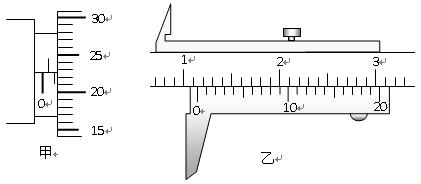
(2)在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.
①实验对两次拉伸橡皮条的要求中,下列哪些说法是正确的?
A.将橡皮条拉伸相同长度即可
B.将橡皮条沿相同方向拉到相同长度
C.将弹簧秤都拉伸到相同刻度
D.将橡皮条和绳的结点拉到相同位置
②同学们在操作过程中有如下议论,其中对减小实验误差有益的说法是?
A.两细绳必须等长
B.弹簧秤、细绳、橡皮条都应与木板平行
C.用两弹簧秤同时拉细绳时两弹簧秤示数之差应尽可能大
D.拉橡皮条的细绳要长些,标记同一细绳方向的两点要远些
(3)在“探究弹簧弹力大小与伸长量的关系”实验中,甲、乙两位同学选用不同的橡皮绳代替弹簧,为测量橡皮绳的劲度系数,他们在橡皮绳下端面依次逐个挂下钩码(每个钩码的质量均为m=0.1kg,取g=10m/s2),并记录绳下端的坐标X i加(下标i表示挂在绳下端钩码个数).然后逐个拿下钩码,同样记录绳下端的坐标Xi减,绳下端面坐标的值Xi=(Xi加+X i减)/2的数据如下表:
挂在橡皮绳下端的钩码个数
| 橡皮绳下端的坐标(X/mm)
|
甲
| 乙
|
1
| 216.5
| 216.5
|
2
| 246.7
| 232.
|
3
| 284.0
| 246.5
|
4
| 335.0
| 264.2
|
5
| 394.5
| 281.3
|
6
| 462.0
| 301.0
|
①同一橡皮绳的X加?X减(大于或小于);
②?同学的数据更符合实验要求(甲或乙);
③某同学选择一组数据用作出拉力F与该变量(Xn-X1)的图像,则由图像可得该橡皮绳的劲度系数k=____________N/m;
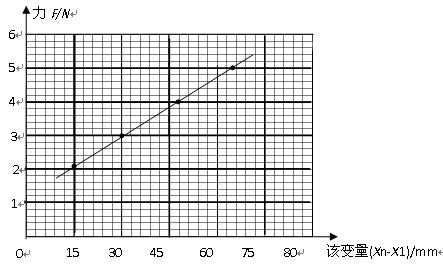
④为了更好的测量劲度系数,在选用钩码时需考虑的因素有哪些(写一种即可)?
参考答案:(1)1.234—1.237mm? 1.145cm
(2)①BD?②BD
(3)①小于?②乙
③58----60(N/m)
④尽可能使伸长量在弹性范围内,同时有足够大的伸长量,以减小长度测量的误差。
本题解析:略
本题难度:简单