1、计算题 A、B为一平行板,板长为l,两板间距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里。一个质量为m,带电荷量为+q的带电粒子以一定初速度沿A、B两板中线且垂直于磁感线方向射入磁场中,粒子恰好从A板的右边界飞出。粒子重力不计。求:
(1)粒子在磁场中运动的轨道半径r和射入磁场的初速度v0各是多少?
(2)粒子在磁场中运动的时间t是多少?
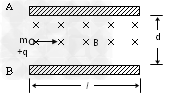
参考答案:解:(1)设粒子做圆周运动的圆心为O(如图)
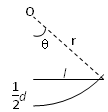
由几何条件可知:r2=l2+(r-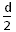 )2?①
)2?①
解之得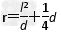
由牛顿第二定律可得:qv0B=m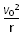 ?②
?②
解①、②式得v0=
(2)设粒子从磁场飞出时,转过的圆心角为θ,粒子做圆周运动的周期为T,则有
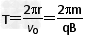 ?③
?③
tgθ=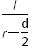 ?④
?④
t=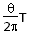 ?⑤
?⑤
解①、③、④、⑤得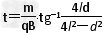 或
或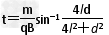
本题解析:
本题难度:一般
2、计算题 (20分)如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场,质量为m、电荷量为-q(q>0)的粒子1以速度v1=v0从O点垂直射入磁场,其方向与MN的夹角 =30o;质量为m、电荷量为+q的粒子2以速度
=30o;质量为m、电荷量为+q的粒子2以速度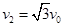 也从O点垂直射入磁场,其方向与MN的夹角
也从O点垂直射入磁场,其方向与MN的夹角 =60o。已知粒子l、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用。
=60o。已知粒子l、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用。
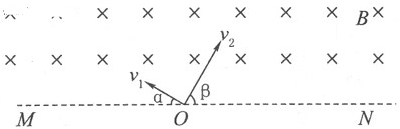
(1)请画出粒子1和2在磁场中运动的轨迹;
(2)求两粒子在磁场边界上的穿出点A、B之间的距离d;
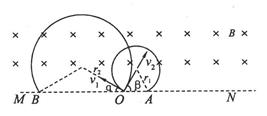
(3)求两粒子进入磁场的时间间隔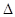 t;
t;
(4)若MN下方有一匀强电场,使两粒子在电场中相遇,其中的粒子1做匀加速直线运动。求电场强度E的大小。
参考答案:
本题解析:(1)如图所示(2分)
(2)粒子在匀强磁场中做匀速圆周运动
 ----------------------------------------------------------------(2分)
----------------------------------------------------------------(2分)
粒子1射出点A与O点的距离 -------------------(1分)
-------------------(1分)
粒子2射出点B与O点的距离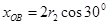 -------------------(1分)
-------------------(1分)
故
代入数据得: --------------------------------------------------(2分)
--------------------------------------------------(2分)
(3)粒子做圆周运动的周期 --------------------------------(2分)
--------------------------------(2分)
设粒子1在磁场中转过的圆心角为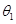
则运动的时间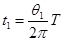 ------------------------------------------(1分)
------------------------------------------(1分)
设粒子2在磁场中转过的圆心角为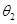
则运动的时间 ------------------------------------------(1分)
------------------------------------------(1分)
所以 ---------------------------------------------(2分)
---------------------------------------------(2分)
(4)由题意得,电场强度的方向应与粒子1穿出磁场方向相反,则粒子1做们加速直线运动,粒子2做类平抛运动。

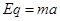 --------------------------------------------------------------(1分)
--------------------------------------------------------------(1分)
 ---------------------------------------(2分)
---------------------------------------(2分)
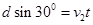 ---------------------------------------------------------(1分)
---------------------------------------------------------(1分)
解得: ----------------------------------------------------(2分)
----------------------------------------------------(2分)
本题难度:一般
3、简答题
(1)求两粒子在磁场中运动的时间之比;
(2)求两粒子在磁场中的运动速率之比;
(3)求两粒子在磁场中运动的向心加速度之比。
参考答案:(1) ?(2)
?(2)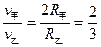 ?(3)
?(3)
本题解析:(1)带电粒子做圆周运动的周期  ?(1分)
?(1分)
所以  ?(1分)
?(1分)
由几何关系,从p点射出磁场的甲粒子做圆周运动的圆心角  (1分)
(1分)
从q点射出磁场的乙粒子做圆周运动的圆心角  ?(1分)
?(1分)
故两粒子在磁场中运动时间之比  ?(1分)
?(1分)
(2)粒子在磁场中运动半径  ?(1分)
?(1分)
设ac边的长度为L,由几何关系:
从p点射出磁场的粒子做圆周运动的半径 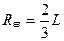 ?(1分)
?(1分)
从q点射出磁场的粒子做圆周运动的半径  ?(1分)
?(1分)
故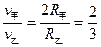 ?(3分)
?(3分)
(3)由 ?(2分)
?(2分)
 ?(2分)
?(2分)
本题难度:简单
4、简答题 如图所示,一种β射线管由平行金属板A、B和平行于金属板的细管C组成,放射源S在A极板左端,可以向各个方向发射不同速度的β粒子.若金属板长为L,金属板间距为
L,细管C与两金属板等距,已知β粒子电荷量为-e,质量为m.求:
(1)当A、B板间加上垂直纸面向外的磁感应强度为B的匀强磁场时,能从细管C水平射出β粒子速度大小;
(2)当A、B板间加电压U时,放射源S射出的β粒子速度大小为多少时,才难从细管C水平射出.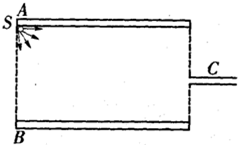
参考答案:
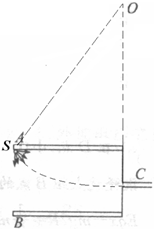
(1)加匀强磁场B时,?粒子在磁场中做匀速圆周运动,如图,圆心在O点,
由几何知识得:R2=L2+(R-14L)2R=178L①
洛伦兹力提供向心力?evB=mv2R②
由①②整理得?v=17eBL8m
(2)加电压U,A、B板间为匀强电场.β粒子从放射源S发射,
从细管C水平射出的逆过程为类平抛运动,设β粒子从放射源
S发射的速度为v,从细管C水平射出的速度为v0,则
水平方向?x=L=v0t
竖直方向?y=L4=12at2
a=Eem
E=2UL
联立以上各式求得v0=2
本题解析:
本题难度:一般
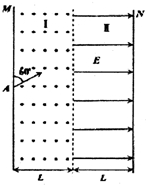
5、简答题 如图所示,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场,条形区域Ⅱ(含Ⅰ、Ⅱ区域分界面)存在水平向右的匀强电场,电场强度为E,磁场和电场宽度均为L且足够长,M、N为涂有荧光物质的竖直板.现有一束带正电的粒子从A处连续不断地射入磁场,入射方向与M板成60°夹角且与纸面平行,粒子束由两部分组成,一部分为速度大小为v的低速粒子,另一部分为速度大小为3v的高速粒子,当I区中磁场较强时,M板出现两个亮斑,缓慢减弱磁场的强度,直至M板亮斑刚刚相继消失为止,此时观察到N板有两个亮斑.已知粒子质量为m,电量为+q,不计粒子重力和相互作用力,求:
(1)M板上的亮斑刚刚相继消失时,I区磁感应强度的大小;
(2)到达N板下方亮斑的粒子在磁场中运动的时间;
(3)N板两个亮斑之间的距离.
参考答案:(1)此时低速粒子速度恰好与两场交界相切且与电场方向垂直,在磁场中运动半径为R1
由牛顿第二定律得:qvB=mv2R1,①
由几何知识可得:R1+R1cos60°=L②
由①②解得:B=3mv2qL③
(2)低速质子在磁场中运动时间t=2πR13v④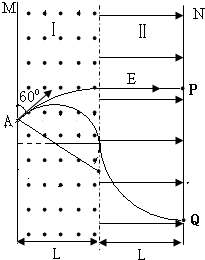
因t=13T
则由②④得t=4πL9v⑤
(3)高速质子轨道半径R2=3R1⑥
由几何关系知此时沿电场线方向进入电场,到达N板时与A点竖直高度差
h1=R2(1-sin60°)⑦
低速质子在磁场中偏转距离
h2=R1sin60°⑧
在电场中偏转距离
h3=vt′⑨
在电场中时间t′,L=12at′2⑩
eE=ma(11)
由②⑥⑦⑧⑨⑩(11)得
亮斑PQ间距h=h1+h2+h3=(2-2
本题解析:
本题难度:一般