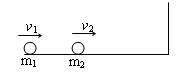
1、计算题 如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2 m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103 V/m。一不带电的绝缘小球甲,以速度υ0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞。已知甲、乙两球的质量均为m=1.0×10-2 kg,乙所带电荷量q=2.0×10-5 C,g取10 m/s2。(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)
(1)甲乙两球碰撞后,乙恰能通过轨道的最高点D,求乙在轨道上的首次落点到B点的距离;
(2)在满足(1)的条件下,求的甲的速度υ0;
(3)若甲仍以速度υ0向右运动,增大甲的质量,保持乙的质量不变,求乙在轨道上的首次落点到B点的距离范围。

参考答案:解:(1)在乙恰好能通过轨道的最高点的情况下,设乙到达最高点的速度为 ,乙离开D点达到水平轨道的时间为t,乙的落点到B点的距离为
,乙离开D点达到水平轨道的时间为t,乙的落点到B点的距离为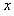 ,则
,则
? 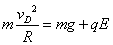 ?①
?①
?  ?②
?②
?  ?③
?③
? 联立①②③得: ④
④
(2)设碰撞后甲、乙的速度分别为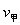 、
、 ,根据动量守恒和机械能守恒定律有:?
,根据动量守恒和机械能守恒定律有:?
?  ?⑤?
?⑤?
?  ?⑥
?⑥
? 联立⑤⑥得: ⑦
⑦
? 由动能定理得: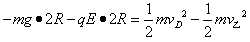 ⑧
⑧
? 联立①⑦⑧得: ⑨
⑨
(3)设甲的质量为M,碰撞后甲、乙的速度分别为 、
、 ,根据动量守恒和机械能守恒定律有:
,根据动量守恒和机械能守恒定律有:
?  ?⑽?
?⑽?
?  ?⑾
?⑾
? 联立⑽⑾得: ?⑿
?⑿
? 由⑿和 ,可得:
,可得: <2v0?⒀
<2v0?⒀
? 设乙球过D点的速度为 ,由动能定理得
,由动能定理得
?  ?⒁
?⒁
? 联立⑨⒀⒁得: <
< ?⒂
?⒂
? 设乙在水平轨道上的落点到B点的距离为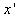 ,则有
,则有 ?⒃
?⒃
? 联立②⒂⒃得: <
< <
<
本题解析:
本题难度:困难
2、计算题 如图甲所示,物块A、B的质量分别是mA=4.0 kg和mB=3.0 kg,用轻弹簧拴接放在光滑的水平地面上,物块B右侧与竖直墙相接触。另有一物块C从t=0时以一定速度向右运动,在=4 s时与物块A相碰,并立即与A粘在一起不再分开,物块C的v-t图像如图乙所示。求:
(1)物块C的质量mC;
(2)墙壁对物块B的弹力在4s到12 s的时间内对B做的功W及对B的冲量I的大小和方向;
(3)B离开墙后的过程中弹簧具有的最大弹性势能Ep。

参考答案:解:(1)由乙图知,C与A碰前速度为v1=9 m/s,碰后速度为v2=3 m/s,C与A碰撞过程动量守恒,则有
mCv1=(mA+mC)v2
解得mC=2 kg
(2)墙对物块B不做功,所以W=0
由图乙知,12 s末A和C的速度为v3=-3 m/s,在4s 到12 s内墙对B的冲量为
I=(mA+mC)v"3-(mA+mC)v3
所以I= -36 N·s,方向向左
(3)12 s末B离开墙壁,之后A、B、C及弹簧组成的系统动量和机械能守恒,且当A、C与B速度相等时弹簧弹性势能最大
(mA+mC)v3=(mA+mB+mC)v4

解得Ep=9 J
本题解析:
本题难度:困难
3、选择题 质量相等的两个小球A、B,在光滑水平面上沿同一直线向同一方向运动.A球初动量为7 kg·m/s,B球的初动量为5 kg·m/s.当A追上B球发生碰撞后,A、B两球动量的可能值为
A.pA=6 kg·m/s? pB=6 kg·m/s
B.pA=3 kg·m/s? pB=9 kg·m/s
C.pA=-2 kg·m/s? pB=14 kg·m/s
D.pA=-4 kg·m/s? pB=10 kg·m/s
参考答案:A
本题解析:该类题中发生的物理过程,应同时满足:碰撞前后系统动量守恒,即Δp=0,碰撞前后系统的动能不能增加,即ΔEk≤0.分析A、B、C、D四个选项,可知D不满足动量守恒,故D不正确.A、B、C三个选项均满足动量守恒,但B、C选项中,碰撞后系统的动能均大于碰撞前的系统动能,故B、C不正确,只有A正确
本题难度:简单
4、选择题 如图为中国 队员投掷冰壶的镜头.在某次投掷
队员投掷冰壶的镜头.在某次投掷 中,冰壶运动一段时间后以0.4 m/s的速度与对方的静止
中,冰壶运动一段时间后以0.4 m/s的速度与对方的静止 冰壶发生正碰,碰后对方的冰壶以0.3 m/s的速度
冰壶发生正碰,碰后对方的冰壶以0.3 m/s的速度 向前滑行.若两冰壶质量相等,规定向前运动方向为正方向,则碰后中国队冰壶获得的速度为
向前滑行.若两冰壶质量相等,规定向前运动方向为正方向,则碰后中国队冰壶获得的速度为

[? ]
A.-0.1 m/s
B.-0.7 m/s
C.0.1 m/s
D.0.7 m/s
参考答案:C
本题解析:
本题难度:简单
5、计算题 (选修模块3-5)(15分)
小题1:下列说法正确的有?(?)
A.卢瑟福的α粒子散射实验可以估测原子核的大小
B.氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动加速度增大
C.物质波是一种概率波,在微观物理学中不可以用“轨迹”来描述粒子的运动
D.若氢原子从 n =" 6" 能级向 n =" 1" 能级跃迁时辐射出的光不能使某金属发生光电效应,则氢原子从 n =" 6" 能级向 n =" 2" 能级跃迁时辐射出的光能使该金属发生光电效应
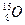 注入人体,
注入人体,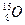 在人体内衰变放出的正电子与人体内的负电子相遇而湮灭,转化为一对γ光子,被探测器探测到,并经计算机处理后产生清晰的图象.根据PET的原理,
在人体内衰变放出的正电子与人体内的负电子相遇而湮灭,转化为一对γ光子,被探测器探测到,并经计算机处理后产生清晰的图象.根据PET的原理,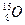 在人体内衰变的方程式是??;在PET中,
在人体内衰变的方程式是??;在PET中,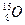 的主要用途是作为?.
的主要用途是作为?.