1、选择题  如图所示，两平行板竖直放置，A、B两小孔正对，两极板间所加电压为500 V，一个动能为400 eV的电子从A孔沿垂直于板面方向射入电场，经一段时间后离开电场，则电子离开电场时动能为（?）

A.900 Ev? B.500 eV? C.400 eV? D.100 eV

参考答案：C

本题解析：由图可知：电子在匀强电场中做匀减速运动，当电子克服电场力做功等于400 eV时，电子的速度便减小到0，之后返回，当到后返A点时，电场力做功为0，由动能定理知：电子的动能仍然不变，故应选C.本题很容易错选D，那是由于没有考虑电子在电场中减速到0后会原路返回，而直接套公式eU=Ek0-Ek，即500 eV="400" eV-Ek，所以Ek="-100" eV，便得到错误结果D.

本题难度：简单

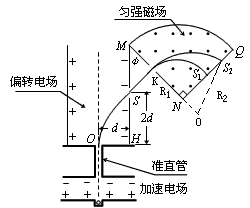
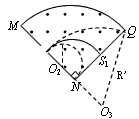
2、计算题  如图，离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管，垂直射入匀强偏转电场，偏转后通过极板HM上的小孔S离开电场，经过一段匀速直线运动，垂直于边界MN进入磁感应强度为B的匀强磁场。已知HO＝d，HS＝2d，∠MNQ＝90°。（忽略粒子所受重力）
（1）求偏转电场场强E0的大小以及HM与MN的夹角φ；
（2）求质量为m的离子在磁场中做圆周运动的半径；
（3）若质量为4m的离子垂直打在NQ的中点S1处，质量为16m的离子打在S2处。求S1和S2之间的距离以及能打在NQ上的正离子的质量范围。

参考答案：解：（1）正离子被电压为U0的加速电场加速后速度设为V1，设对正离子，应用动能定理有
eU0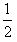＝mV12
正离子垂直射入匀强偏转电场，作类平抛运动
受到电场力F＝qE0、产生的加速度为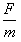a＝，即a＝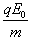
垂直电场方向匀速运动，有2d＝V1t
沿场强方向：Y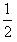＝at2
联立解得E0＝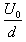
又tanφ＝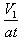
解得φ＝45°
（2） 正离子进入磁场时的速度大小为V2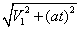＝，正离子在匀强磁场中作匀速圆周运动，由洛仑兹力提供向心力，qV2B＝
解得离子在磁场中做圆周运动的半径R＝2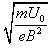
（3）根据R＝2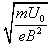可知
质量为4m的离子在磁场中的运动打在S1，运动半径为R1＝2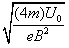
质量为16m的离子在磁场中的运动打在S2，运动半径为R2＝2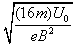
又ON＝R2－R1
由几何关系可知S1和S2之间的距离ΔS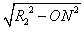＝－R1
联立解得ΔS＝4(－)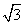
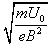
由R′2＝(2R1)2+(R′－R1)2，解得R′＝R1
再根据R1＜R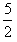＜R1，解得m＜mx＜25m

本题解析：

本题难度：困难

3、简答题  

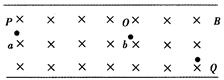
两水平放置的金属板间存在一竖直方向的匀强电场和垂直纸面向里的匀强磁场，磁感应强度为B，一质量为4m，带电量为-2q的微粒b正好悬浮在板间正中间O点处，另一质量为m，带电量为 +q的微粒a，从p点以水平速度v0(v0未知)进入两板间，正好做匀速直线运动，中途与b碰撞。：
小题1:匀强电场的电场强度E为多大?微粒a的水平速度为多大?
小题2:若碰撞后a和b结为一整体，最后以速度0.4v0从Q点穿出场区，求Q点与O点的高度差?
小题3:若碰撞后a和b分开，分开后b具有大小为0.3v0的水平向右速度，且带电量为-q/2，假如O点的左侧空间足够大，则分开后微粒a的运动轨迹的最高点与O点的高度差为多大?
??

参考答案：
小题1:　E =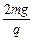??v0 =
小题2:h = 0.9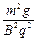
　?
小题3:ha = 2R =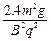

本题解析：
小题1:　对b微粒，没与a微粒碰撞前只受重力和电场力，则有2qE = 4mg
∴E =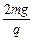
对a微粒碰前做匀速直线运动，则有
Bqv0 = Eq + mg?∴v0 =
小题2:碰撞后，a、b结合为一体，设其速度为v
由动量守恒定律得
mv0 = 5mv?∴v =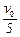
碰后的新微粒电量为– q
设Q点与O点高度差为h
由动能定理：
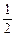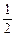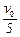5mgh – Eqh =5m (0.4v0) –5m ()2
∴h = 0.9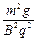
小题3:碰撞后，a、b分开，则有
mv0 = mva + 4mvb?vb =" 0.3" v0，得va =" –" 0.2v0
a微粒电量为 – q / 2，受到的电场力为
E ·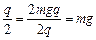?∴F电 = mg
故a微粒做匀速圆周运动，设半径为R
B | va |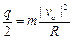?∴R =
a的最高点与O点的高度差ha = 2R =。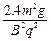

本题难度：简单

4、选择题  如图为一匀强电场，某带电粒子从A点运动到B点，在这一运动过程中克服重力做的功为3.0J，电场力做的功为2.0J。则下列说法正确的是(  )

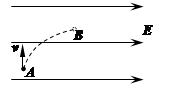
A．粒子带正电
B．粒子在A点的电势能比在B点少2.0J
C．粒子在A点的机械能比在B点少1.0J
D．粒子在A点的动能比在B点多1.0J