1、选择题  如图所示，边长为L的正方形线圈abcd，其匝数为n，总电阻为r，外电路的电阻为R，ab的中点和cd的中点的连线OO′恰好位于匀强磁场的边界线上，磁场的磁感应强度为B.若线圈从图示位置开始，以角速度ω绕OO′轴匀速转动，则以下判断中正确的是

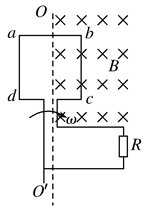
A．闭合电路中感应电动势的瞬时值表达式e＝nBL2ωsinωt
B．在t＝时刻，磁场穿过线圈的磁通量为零，此时磁通量随时间变化最快
C．从t＝0时刻到t＝时刻，电阻R上产生的热量为Q＝n2B2L4πωR/16(R+r)2
D．从t＝0时刻到t＝时刻，通过R的电荷量q＝BL2/2R

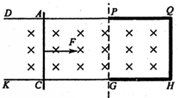
2、简答题  如图所示，相距为L的两条足够长光滑平行金属导轨固定在水平面上，导轨由两种材料组成．PG右侧部分单位长度电阻为r0，且PQ=QH=GH=L．PG左侧导轨与导体棒电阻均不计．整个导轨处于匀强磁场中，磁场方向垂直于导轨平面向下，磁感应强度为B．质量为m的导体棒AC在恒力F作用下从静止开始运动，在到达PG之前导体棒AC已经匀速．
（1）求当导体棒匀速运动时回路中的电流；
（2）若导体棒运动到PQ中点时速度大小为v1，试计算此时导体棒加速度；
（3）若导体棒初始位置与PG相距为d，运动到QH位置时速度大小为v2，试计算整个过程回路中产生的焦耳热．

3、计算题  如图所示，一对平行光滑轨道放置在水平面上，两轨道间距L＝0.20m，电阻R＝10Ω，有一质量为m＝1kg的金属棒平放在轨道上，与两轨道垂直，金属棒及轨道的电阻皆可忽略不计，整个装置处于垂直轨道平面向下的匀强磁场中，磁感应强度B=5T，现用一外力F沿轨道方向拉金属棒，使之做匀加速运动，加速度a＝1m/s2，试求：
（1）力F与时间t的关系。
（2）F＝3N时，电路消耗的电功率P。
（3）若外力F的最大值为5N，为求金属棒运动所能达到的最大速度，某同学解法为：先由（1）中的结果求出F＝5N时的时间t，然后代入求解。指出该同学解法的错误之处，并用正确的方法解出结果。

4、选择题  关于磁感线，以下说法中正确的是
A.磁感线上各点的切线方向就是该点的磁感应强度方向
B.磁感线是磁场中真实存在的曲线
C.磁感线总是从磁体的N极发出终止于磁体的S极
D.沿着磁感线方向，磁场越来越弱

5、计算题  如图甲所示，水平面上的两光滑金属导轨平行固定放置，间距d＝0.5 m，电阻不计，左端通过导线与阻值R ＝2 W的电阻连接，右端通过导线与阻值RL ＝4 W的小灯泡L连接．在CDEF矩形区域内有竖直向上的匀强磁场，CE长l ="2" m，有一阻值r ="2" W的金属棒PQ放置在靠近磁场边界CD处（恰好不在磁场中）．CDEF区域内磁场的磁感应强度B随时间变化如图乙所示．在t＝0至t＝4s内，金属棒PQ保持静止，在t＝4s时使金属棒PQ以某一速度进入磁场区域并保持匀速运动．已知从t＝0开始到金属棒运动到磁场边界EF处的整个过程中，小灯泡的亮度没有发生变化，求：
（1）通过小灯泡的电流．
（2）金属棒PQ在磁场区域中运动的速度大小．