1、简答题 一九二三年美国物理学家迈克耳逊用旋转棱镜法较准确的测出了光速,其过程大致如下,选择两个距离已经精确测量过的山峰(距离为L),在第一个山峰上装一个强光源S,由它发出的光经过狭缝射在八面镜的镜面1上,被反射到放在第二个山峰的凹面镜B上,再由凹面镜B反射回第一个山峰,如果八面镜静止不动,反射回来的光就在八面镜的另外一个面3上再次反射,经过望远镜,进入观测者的眼中.(如图所示)?如果八面镜在电动机带动下从静止开始由慢到快转动,当八面镜的转速为ω时,就可以在望远镜里重新看到光源的像,求光传播速度的表达式?
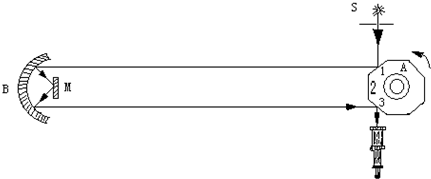
参考答案:周期T=2πω,我们要看到光源,只要八面型棱镜的镜面在光反射回来时位置与图上所示重合,即转过了nπ4ω,也就是经历了八分之一的n倍的时间.而光速过大,试验条件只可能让我们做到在八分之一周期的时间内看到光返回.那么根据v=st可得,光速c=2Lπ4ω=8Lωπ,
答:光传播速度的表达式C=8Lωπ.
本题解析:
本题难度:一般
2、选择题 不定项选择
光在某种玻璃中的速度是 ×108m/s,要使光由空气射入这种玻璃,且使折射光线与反射光线之间的夹角为90°,则入射角应是( ? )
×108m/s,要使光由空气射入这种玻璃,且使折射光线与反射光线之间的夹角为90°,则入射角应是( ? )
A.30°
B.60°
C.45°
D.90°
参考答案:B
本题解析:
本题难度:一般
3、填空题 .一点光源S经平面镜M成像于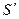 ,人眼在P点可以观察到
,人眼在P点可以观察到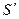 ,如右图所示.若S、M之间放一不太大的遮光板N,则? (? )
,如右图所示.若S、M之间放一不太大的遮光板N,则? (? )

A.S不能在平面镜M中成像
B.S仍能在平面镜M中成像
C.人眼观察到像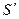 的亮度将减小
的亮度将减小
D.人眼观察到像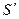 的亮度将不变
的亮度将不变
参考答案:BD
本题解析:若在S、M之间放一不太大的遮光板N,点光源S发的光仍能射到镜面上,只是比不放遮光板N要少,因此S仍能在平面镜M中成像,A错B对.因人眼在P点,放不放遮光板,经镜面反射进入人眼的光线不变,故人眼观察到像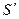 的亮度将不变,C错D对.
的亮度将不变,C错D对.
本题难度:简单
4、选择题 如图所示,两平面镜互相垂直交于棱l,入射光a的两次反射光线依次是b和c,若以l为轴使两平面镜顺时针转一个小的角度α,不动入射光线a,新的两次反射光线分别是b"和c",则
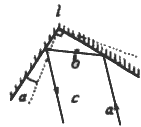
[? ]
A.b"与b夹角为α
B.b"与b夹角为2α
C.c"与c同向平行
D.c"与c不平行
参考答案:BC
本题解析:
本题难度:简单
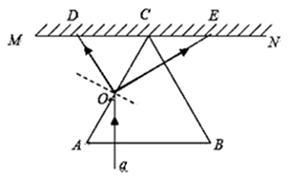
5、作图题 (10分)、(10分)如图所示,在MN的下方足够大的空间是玻璃介质,其折射率为n=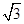 ,玻璃介质的上边界MN是屏幕。玻璃中有一正三角形空气泡,其边长l=40 cm,顶点与屏幕接触于C点,底边AB与屏幕平行。一束激光a垂直于AB边射向AC边的中点O,结果在屏幕MN上出现两个光斑。
,玻璃介质的上边界MN是屏幕。玻璃中有一正三角形空气泡,其边长l=40 cm,顶点与屏幕接触于C点,底边AB与屏幕平行。一束激光a垂直于AB边射向AC边的中点O,结果在屏幕MN上出现两个光斑。
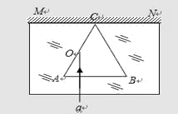
①求两个光斑之间的距离L.
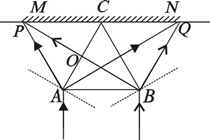
②若任意两束相同激光同时垂直于AB边向上入射进入空气泡,求屏幕上相距最远的两个光斑之间的距离。
参考答案:40cm ?80cm
本题解析:①画出光路图如图所示?(1分)
在界面AC,a光的入射角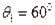 (1分)
(1分)
由光的折射定律有: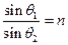 ? (1分)?代入数据求得折射角
? (1分)?代入数据求得折射角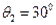 ? (1分)
? (1分)
由光的反射定律得反射角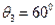 ? (1分)
? (1分)
 ?
?
由几何关系易得:ΔODC是边长为l/2的正三角形,ΔCOE为等腰三角形,CE=OC=l/2
故两光斑之间的距离L=DC+CE=l=40cm? (2分)
②光路图(1分)屏幕上相距最远的两个光斑之间的距离为PQ=2L=80cm? (2分)
本题难度:一般