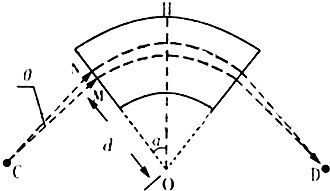
1、简答题  如图为一种质谱仪工作原理示意图．在以O为圆心，OH为对称轴，夹角为2α的扇形区域内分布着方向垂直于纸面的匀强磁场．对称于OH轴的C和D分别是离子发射点和收集点．CM垂直磁场左边界于M，且OM=d．现有一正离子束以小发散角（纸面内）从C射出，这些离子在CM方向上的分速度均为v0．若该离子束中比荷为

参考答案：


（1）
设沿CM方向运动的离子在磁场中做圆周运动的轨道半径为R
由　? qv0B=mv20R?
又? R=d
得? B=mv0qd
磁场方向垂直纸面向外
（2）
设沿CN运动的离子速度大小为v，在磁场中的轨道半径为R′，运动时间为t
由vcosθ=v0
得v=v0cosθ
R′=mvqB
=dcosθ
离子在磁场中做匀速圆周运动的周期T=2πmqB
t=T×θ+απ
=2(θ+α)v0d
（3）
设圆心为A，过A做AB垂直NO，
可以证明NM=BO
∵NM=CMtanθ
又∵BO=ABcotα
=R′sinθcotα
=dcosθsinθcotα
∴CM=dcotα

本题解析：

本题难度：一般

2、选择题  做匀速圆周运动的物体，下列不变的物理量是
[? ]
A．速度
B．速率
C．角速度
D．周期

参考答案：BCD

本题解析：

本题难度：简单

3、计算题  (12分)一个圆盘在水平面内匀速转动，盘面上距圆盘中心0．10m的位置有一个质量为0．10kg的小物体在随圆盘一起做匀速圆周运动，如图所示，

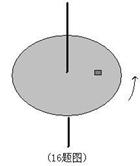
（1）当w=4rad／s小物体所受向心力的大小？方向如何？
（2）当小物体与圆盘之间动摩擦因素为0．25，求圆盘最大的角速度？                                    

参考答案：（1）0.16N  方向：指向圆心（2）5rad／s

本题解析：（1）小物体所受向心力的大小
F=mw2r=0．16N………………………………………（4分）         
方向：指向圆心……………………………………（2分）
（2）由摩擦力提供向心力得
цmg=mw2r……………………………………………（4分）     
得w=5rad／s……………………………………… （2分）

本题难度：一般

4、计算题  如图所示，在匀速转动的圆盘上，沿半径方向放置以细线相连的质量均为m的A、B两个小物块，A离轴心r1＝20 cm，B离轴心r2＝30 cm，A、B与盘面间相互作用的最大静摩擦力为其重力的0.4倍．求：

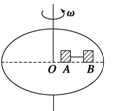
(1)若细线上没有张力，圆盘转动的角速度ω应满足什么条件？
(2)欲使A、B与盘面间不发生相对滑动，则盘转动的最大角速度多大？
(3)当圆盘转速达到A、B刚好不滑动时，烧断细绳，则A、B将怎样运动？(g取10 m/s2)

参考答案：(1) 当ω≤ω0＝3.6 rad/s时，细线上不会有张力．(2) 4.0 rad/s.

本题解析：(1)当物块B所需向心力FB≤Ffm时，细线上张力为零．随着角速度的增大，当FB＝Ffm时，有kmg＝mω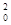r2，
得ω0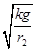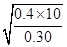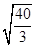＝＝＝＝3．6 rad/s.
当ω≤ω0＝3.6 rad/s时，细线上不会有张力．
(2)当A、B所受静摩擦力均达到最大静摩擦力时，圆盘的角速度达到最大值ωm，超过ωm时，A、B将相对圆盘滑动．(设细线中张力为T.)
对A有kmg－T＝mωm2·r1，
对B有kmg＋T＝mωm2·r2，
解得ωm＝＝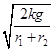
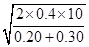
＝4.0 rad/s.
(3)烧断细线时，A做圆周运动所需向心力FA＝mωm2r1＝3.2 N，最大静摩擦力为4 N，A物体随盘一起转动．B此时所需向心力为FB＝mωm2r2＝4.8 N，大于它的最大静摩擦力4 N，因此B物体将沿一条曲线运动，离圆心越来越远．
两物体做圆周运动的向心力由沿径向方向的合力提供，及最大静摩擦力提供，第二问中分别以两小球为研究对象，绳子的拉力和静摩擦力的合力提供向心力列式求解

本题难度：一般

5、选择题  关于匀速圆周运动，下列说法正确的是：[? ]
A．线速度不变
B．加速度不变
C．周期不变
D．合外力等于向心力

参考答案：CD

本题解析：匀速圆周运动的速度大小恒定，但是方向在时时刻刻变化，A错误，加速度大小恒定，方向时时刻刻指向圆心，B错误，匀速圆周运动的周期是一个定值，恒定不变，C正确，匀速圆周运动由于速度大小不变，所以切向加速度为零，只有向心加速度，故合力等于向心力，D正确
故选CD
点评：匀速圆周运动速度大小不变，方向变化，是变速运动．加速度方向始终指向圆心，加速度是变化的，是变加速运动．向心力方向始终指向圆心，是变化的．

本题难度：简单