1、计算题  (15分)如图所示，相距L＝0.4m、电阻不计的两平行光滑金属导轨水平放置，一端与阻值R＝0.15Ω的电阻相连，导轨处于磁感应强度B＝0.5T的匀强磁场中，磁场方向垂直于导轨平面。质量m＝0.1kg、电阻r＝0.05Ω的金属棒置于导轨上，并与导轨垂直。t＝0时起棒在水平外力F作用下以初速度v0＝2m/s、加速度a＝1m/s2沿导轨向右匀加速运动。求：

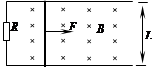
⑴t＝1s时回路中的电流；
⑵t＝1s时外力F大小；
⑶第1s内通过棒的电荷量。

参考答案：⑴I＝3A；⑵F＝0.7N；⑶q＝2.5C

本题解析：⑴t＝1s时，棒的速度为：v1＝v0＋at＝3m/s
此时由于棒运动切割产生的电动势为：E＝BLv1＝0.6V
根据闭合电路欧姆定律可知，此时回路中的感应电流为：I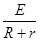＝＝3A
⑵对棒，根据牛顿第二定律有：F－ILB＝ma
解得t＝1s时外力F大小为：F＝ILB＋ma＝0.7N
⑶在t＝1s时间内，棒的位移为：x＝v0t＋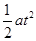
根据法拉第电磁感应定律可知，在这段时间内，棒切割平均感应电动势为：＝
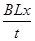
根据闭合电路欧姆定律可知，在这段时间内，回路中的平均感应电流为：＝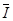
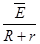
在第1s时间内，通过棒的电荷量为：q＝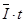
联立以上各式解得：q＝2.5C

本题难度：一般

2、计算题  在一条平直的公路上，乙车以10m/s的速度匀速行驶，甲车在乙车的后面做初速度为15m/s，加速度大小为0.5m/s2的匀减速运动，则两车初始距离L满足什么条件时，可以使
(1)两车不相遇；
(2)两车只相遇一次；
(3)两车能相遇两次（设两车相遇时互不影响各自的运动）。

参考答案：解：设两车速度相等经历的时间为t，则甲车恰能追上乙车时，应有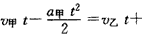L，其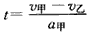，解得L=25m
（1）若L>25m，则两车等速时也未追及，以后间距会逐渐增大，即两车不相遇
（2）若L=25m，则两车等速时恰好追及，两车只相遇一次，以后间距会逐渐增大
（3）若L＜25m，则两车等速时，甲车巳运动至乙车前面，以后还能冉次相遇，即能相遇两次

本题解析：

本题难度：一般

3、计算题  一辆汽车以8m／s的速度匀速行驶且即将通过两个路口。某一时刻汽车距离第一路口的停车线18m，此时第一个路口的绿灯还有2s熄灭，第二个路口的绿灯还8s熄灭。已知两路口停车线间距为100m，该车加速时最大加速度大小为2m/s2；减速时最大加速度大小为7m/s2。该路段允许行驶的最大速度为14m/s。忽略汽车长度，试问：
（1）如果汽车立即做匀加速直线运动，在绿灯熄灭前汽车能否通过第一路口停车线？并说明理由。
（2）如果汽车立即做匀加速直线运动，在绿灯熄灭前汽车能否通过第二路口停车线？并说明理由。
（3）试求汽车从初位置到第二路口停车线停下来所用最短时间。（结果保留一位小数）

参考答案：解：（1）从该时刻起，让汽车以最大速度做匀加速运动，2s内的位移为x，2s内的速度为v，则
X=v0t+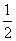a1t2=20m>18m
v=v0+a1t=12m/s<14m/s
所以汽车可以通过第一个路口
（2）设汽车达到最大速度的时间为t1，此段位移为x1，则根据速度公式有
t1=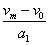=3s
此段位移为x1=v0t1+a1t12=33m
匀速运动到第二个路口停车线的时间为t2，则
X2=d1+d2－x1
t2==6.07s
到达第二个路口的总时间为t总，则
t总=t1+t2=9.07s>8s
所以不能通过第二个路口
（3）设汽车从最大速度状态以最大加速度减速停下所用时间为t3，位移为x3，则
t3==2s
x3=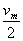t3=14m
匀速运动的位移和时间分别为和，则
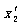=d1+d2－x1－x3
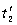==5.1s
总时间t总"=t1+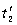+t3=10.1s

本题解析：

本题难度：困难

4、选择题  物体从静止开始做匀加速直线运动，已知第3s内与第2s内的位移之差是6m，则可知(? )?
A．第1 s内的位移为3 m
B．第2s末的速度为12m/s
C．物体运动的加速度为3m/s2
D．物体在前4s内的平均速度为15m/s

参考答案：AB

本题解析：在匀变速直线运动中在相邻的相等的时间内通过的位移差值不变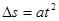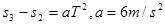，，由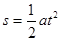可以求出第1s内位移为3m，由v=at可知B对；C错；前4s内的平均速度等于第2s末速度，为12m/s，D错；

本题难度：简单

5、选择题  下列哪个图象能正确地描述出从一楼出发到二十二楼终止的电梯运动情况（　　）
A．
B．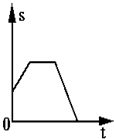
C．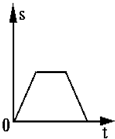
D．

参考答案：电梯在运动的过程中先做加速运动，再做匀速运动，最后做减速运动，位移时间图线的斜率先增大，再不变，最后减小．故A正确，B、C、D错误．
故选A．

本题解析：

本题难度：一般