1、简答题  如图所示，质量为70kg的工人站在岸边通过一滑轮组打捞一块沉没在水池底部的石材，该滑轮组中动滑轮质量为5kg．当工人用120N的力拉滑轮组的绳端时，石材仍沉在水底不动．工人继续增大拉力将石材拉起，在整个提升过程中，石材始终以0.2m/s的速度匀速上升．在石材还没有露出水面之前滑轮组的机械效率为η1，当石材完全露出水面之后滑轮组的机械效率为η2，且η1：η2=63：65．绳重及滑轮的摩擦均可忽略不计，石材的密度
ρ石=2.5×103kg/m3，取g=10N/kg，求：
（1）当人用120N的力拉绳端时，岸边地面对人的支持力为多大；
（2）在石材脱离水池底部至完全露出水面的过程中，地面对人的支持力的最大值与最小值之比；
（3）当石材露出水面之前，人拉绳子的功率；
（4）此人用这个滑轮组提升重物的最大机械效率．

参考答案：
工人的重力：
G人=m人g=70kg×10N/kg=700N，
动滑轮的重力：
G动=m动g=5kg×10N/kg=50N，
未露出水面滑轮组的机械效率：
η=W有W总=(G石-F浮)h?(G石-F浮+G动)h=G石-F浮G石-F浮+G动，
露出水面后滑轮组的机械效率：
η=W有W总=G石h?(G石+G动)h=G石G石+G动，
∵η1：η2=63：65，
即ρ石Vg-ρ水Vgρ石Vg-ρ水Vg+50N：ρ石Vg?ρ石Vg+50N=63：65，
将石块的密度和水的密度代入求得：
V石=0.04m3，
石块的重力：
G石=m石g=ρ石V石g=2.5×103kg/m3×1 0N/kg×0.04m3=1000N，
（1）地面对人的支持力：
F=G人-F拉=700N-120N=580N；
（2）石材在水中，受到水的浮力，此时人的拉力最小，地面对人的支持力最大，
石材受到的浮力：
F浮=ρ水V排g=1×103kg/m3×10N/kg×0.04m3=400N，
F拉1=13 （G石+G动-F浮）=13（1000N+50N-400N）=6503 N，
地面的支持力：
F支1=G人-F拉1=700N-6503 N=14503 N；
石材离开水面，此时人的拉力最大，地面对人的支持力最小，
F拉2=13 （G石+G动）=13（1000N+50N）=350N，
地面的支持力：
F支2=G人-F拉2=700N-350N=350N；
F支1：F支2=14503 N：350N=29：21；
（3）当石材露出水面之前，F拉1=13（G石+G动-F浮）=13 （1000N+50N-400N）=6503 N，
v=3×0.2m/s=0.6m/s
人拉绳子的功率：
P=F拉1v=6503 N×0.6m/s=130W；
（4）重物露出水面后，滑轮组受到的向下的拉力最大，为F=G人=700N，
∵绳重及滑轮的摩擦均可忽略不计，
∴F=13（G物+G动），
∴G物=3F-G动=3×700N-50N=2050N，
η=W有W总=GhFs=GhF?3h=G3F=20503×700≈97.6%．
答：（1）当人用120N的力拉绳端时，岸边地面对人的支持力为580N；
（2）在石材脱离水池底部至完全露出水面的过程中，地面对人的支持力的最大值与最小值之比为29：21；
（3）当石材露出水面之前，人拉绳子的功率为130W；
（4）此人用这个滑轮组提升重物的最大机械效率为97.6%．

本题解析：

本题难度：一般

2、填空题  当汽车沿水平直路以60km/h的速率匀速运动时，发动机的输出功率为P1，若汽车所受阻力与速度的平方成反比，则当汽车以90km/h的速率匀速运动时，发动机的输出功率P2=______P1．

参考答案：当汽车的速度为80km/h时，
60km/h=16.67m/s，
此时由于火车是匀速运动，牵引力和阻力相等，
即F=f=kv2
由P=FV可得，此时的功率P1=fV=kV13，
同理，当火车的速度为90km/h时，
90km/h=25m/s，
由P=FV可得，此时的功率P2=fV=kV23，
所以提速前与提速后机车发动机的功率之比1：1.5
故答案为：1.5

本题解析：

本题难度：一般

3、计算题  物体A的质量m1＝1kg，静止在光滑水平面上的木板B的质量为m2＝0.5kg、长L＝1m，某时刻A以v0＝4m/s的初速度滑上木板B的上表面，为使A不致于从B上滑落，在A滑上B的同时，给B施加一个水平向右的拉力F，若A与B之间的动摩擦因数μ＝0.2，试求拉力F大小应满足的条件。（忽略物体A的大小，取重力加速度g=10m/s2）

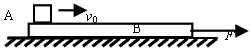
参考答案：解：物体A滑上木板B以后，作匀减速运动，加速度为：aA=μg ①
木板B作加速运动，有：F+μm1g=m2aB ②
物体A不滑落的临界条件是A到达B的右端时，A、B具有共同的速度V1，则： ③
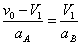又?④
由①③④式，可得：aB=6m/s2
再代入②式得：F= m2aB－μm1g=1N
若F＜1N，则A滑到B的右端时，速度仍大于B的速度，于是将从B上滑落，所以F必须大于等于1N；当F较大时，在A到达B的右端之前，就与B具有相同的速度，之后，A必须相对B静止，才不会从B的左端滑落。
即有：F=（m1+m2）a，μm1g =m1a
所以：F＝3N
若F大于3N，A就会相对B向左滑下
综上分析，力F应满足的条件是：1N≤F≤3N

本题解析：

本题难度：困难

4、填空题  如图所示，质量m=20kg的物体从光滑曲面上高度H=0.8m处释放，到达底端时水平进入水平传送带，传送带由一电动机驱动着匀速向左转动，速率为3m/s．已知物体与传送带间的动摩擦因数μ=0.1．（g取10m/s2）
（1）若两皮带轮之间的距离是6m，物体冲上传送带后就移走光滑曲面，物体将从哪一边离开传送带？通过计算说明你的结论．
（2）若皮带轮间的距离足够大，从m滑上到离开传送带的整个过程中，由于m和传送带间的摩擦而产生了多少热量？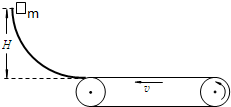

参考答案：（1）物体将从传送带的右边离开．
物体从曲面上下滑时机械能守恒，有mgH=12mv2
解得物体滑到底端时的速度v0=

本题解析：

本题难度：一般

5、计算题  有一个固定竖直放置的圆形轨道，半径为R，由左右两部分组成。如图所示，右半部分AEB是光滑的，左半部分BFA是粗糙的。现在最低点A给一质量为m的小球一个水平向右的初速度v0，使小球沿轨道恰好能过最高点B，且又能沿BFA回到A点，回到A点时对轨道的压力为4mg。不计空气阻力，重力加速度为g。求：

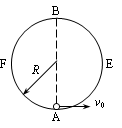
（1）小球的初速度v0大小;
（2）小球沿BFA回到A点时的速度大小;
（3）小球由B经F回到A的过程中克服摩擦力所做的功。

参考答案：（1）（2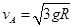）（3）mgR

本题解析：⑴对小球由AEB恰好通过B点，根据牛顿第二定律：
，?
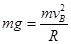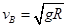根据动能定理 ：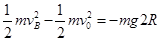
解得：?
⑵由于回到A点时对轨道压力为4mg
根据牛顿第二定律：，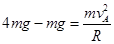
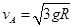
⑶小球由B经F回到A的过程中，根据动能定理：

解得： Wf =mgR

本题难度：简单