1、选择题  跳伞运动员从高度H处由静止下落，假设运动员沿直线运动，经历加速下降和减速下降两个过程，最后以速度v着地．将运动员和伞看成一个系统，总质量为M．在这两个过程中，下列说法正确的是（　　）
A．阻力对系统始终做负功，全程做功等于

参考答案：A、选取运动员从静止到速度为v过程，由动能定理可得：MgH-Wf=12Mv2-0，则有Wf=MgH-12Mv2上式是克服阻力做的功，所以阻力对系统始终做负功，全程做功等于12Mv2-MgH．故A正确；
B、运动员下落中当加速下降时，合力做正功；当减速下降时，合力却做负功．故B错误；
C、重力做功由高度决定，然而在加速过程与减速过程中高度不清楚，所以无法确定大小，故C错误；
D、重力做功由高度决定，然而在加速过程与减速过程中高度不清楚，所以无法确定大小，故D错误；
故选：A

本题解析：

本题难度：简单

2、选择题  ）人站在h高处的平台上，水平抛出一个质量为m的物体，物体落地时的速度为v，以地面为重力势能的零点，不计空气阻力，则有
A．人对小球做的功是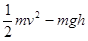
B．人对小球做的功是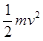
C．小球落地时的机械能是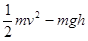
D．小球落地时的机械能是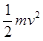

参考答案：AD

本题解析：人对小球做功等于小球动能增量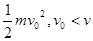，B错；小球从抛出到落地由动能定理A对；小球落地时重力势能为零，只有动能，所以机械能为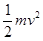，D对；C错；

本题难度：一般

3、计算题  如图所示，光滑绝缘竖直细杆与以正点电荷O为圆心的圆周交于B、C两点。一质量m、带电量为-q的空心小球从杆上A点无初速下落。设AB =" BC" = h，小球滑到B点的速度为试求：

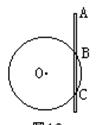
（1）小球滑至C点的速度；
（2）A、C两点的电势差。

参考答案：（1）（2）

本题解析：(1)BC两点是等式点，从B到C过程中，电场力做功为零，由B至C过程，应用动能定理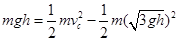：?(2分)解得? 1分)
（2）由A→B应用动能定理，解得（2分）
点评：关键是知道BC两点处于同一个等势面上

本题难度：一般

4、简答题  如图所示，匀强电场的场强E=4V/m，方向水平向左，匀强磁场的磁感应强度B=2T，方向垂直纸面向里．一个质量为m=1g、带正电的小物块A，从M点沿绝缘粗糙的竖直壁无初速度下滑，当它滑行0.8m到N点时就离开壁做曲线运动．当A运动到P点时，恰好处于平衡状态，此时速度方向与水平成45°角，设P与M的高度差H为1.6m．求：
（1）A沿壁下滑时克服摩擦力做的功．
（2）P与M的水平距离s是多少？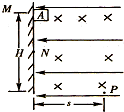

参考答案：

（1）小物体A下落至N点时开始离开墙壁，说明这时小物体A与墙壁之间已无挤压，弹力为零．
故有：qE=qvNB
∴vN=EB=42=2m/s?
对小物体A从M点到N点的过程应用动能定理，这一过程电场力和洛仑兹力均不做功，应有：
mgh-Wf克=12mv2N
∴Wf克=mgh-12mv2N=10-3×10×0.8-12×10-3×22=6×l0-3?（J）?
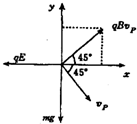
（2）小物体离开N点做曲线运动到达P点时，受力 情况如图所示，由于θ=45°，物体处于平衡状态，建立如图的坐标系，可列出平衡方程．
qBvpcos45°-qE=0?（1）
qBvpsin45°-mg=0?（2）
由（1）得?vp=EBcos45°=2

本题解析：

本题难度：一般

5、选择题  如图所示，质量为m的木块放在倾角为θ的光滑斜面上，已知斜面体与地面之间也是光滑的．在木块下滑的过程中（　　）
A．木块的机械能守恒
B．木块所受的弹力对木块做负功
C．木块和斜面体组成的系统动量守恒
D．斜面体对地面的压力一定小于两个物体的重力之和