1、计算题 ?如图所示,某人距离墙壁10m起跑,向着墙壁冲去,挨上墙之后立即返回出发点。设起跑的加速度为4 m/s2,运动过程中的最大速度为4 m/s,快到达墙根时需减速到零,不能与墙壁相撞。减速的加速度为8 m/s2,返回时达到最大速度后不需减速,保持最大速度冲到出发点.求该人总的往返时间为多少?
参考答案:6.25 s
本题解析:加速阶段:t1= =1 s; (1分)
=1 s; (1分)
s1=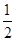 vm
vm xt1=2 m(2分)
xt1=2 m(2分)
减速阶段:t3= =0.5 s;(1分)
=0.5 s;(1分)
s3=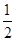 vm
vm xt3=1 m(2分)
xt3=1 m(2分)
匀速阶段:t2= =1.75 s (1分)
=1.75 s (1分)
由折返线向起点(终点)线运动的过程中
加速阶段:t4= =1 s;(1分)
=1 s;(1分)
s4=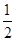 vm
vm xt4=2 m(2分)
xt4=2 m(2分)
匀速阶段:t5=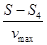 =2 s (1分)
=2 s (1分)
该人总的往返时间为t=t1+t2+t3+t4+t5=6.25 s(1分)
本题难度:简单
2、选择题 如图所示,一足够长的木板在光滑的水平面上以速度v匀速运动,现将质量为m的小物块对准木板的前端轻放,要使木板的运动速度保持不变,在物体开始接触木板到它与木板相对静止的过程中,需要对木板施加水平向右的力F,那么,在此过程中力F做功的数值为(已知物体与木板之间的动摩擦因数为μ)(? )

A.
B.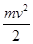
C.mv2
D.2mv2
参考答案:C
本题解析:小物块在木板上滑动的过程中,受重力mg、木板的支持力N和滑动摩擦力f作用,做匀加速直线运动,由于木板足够长,因此最终物块与木板具有相同的速度v,一起匀速运动,往后将不再需要力F作用于木板,设物块加速运动的位移为s1,时间为t,在此过程中,木板运动的位移为s2,根据匀变速直线运动规律和匀速直线运动规律有:s1= ,s2=vt,根据滑动摩擦定律可知:f=μmg,根据动能定理有:fs1=
,s2=vt,根据滑动摩擦定律可知:f=μmg,根据动能定理有:fs1=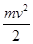 -0,由功的定义式可知,力F做的功为:WF=Fs2,由于开始时木板做匀速运动,因此,根据共点力平衡条件有:F=f,联立以上各式解得:WF=mv2,故选项C正确。
-0,由功的定义式可知,力F做的功为:WF=Fs2,由于开始时木板做匀速运动,因此,根据共点力平衡条件有:F=f,联立以上各式解得:WF=mv2,故选项C正确。
本题难度:一般
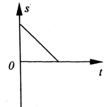
3、选择题 如图所示,表示物体做匀变速直线运动的图象是( )
A.
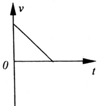
B.
C.
D.

参考答案:A、物体的速度均匀减小,做匀减速直线运动.故A正确.
? B、表示物体向负方向做匀速直线运动.故B错误.
? C、表示物体向正方向做匀速直线运动.故C错误.
? D、速度不随时间变化,表示物体做匀速直线运动.故D错误.
故选A
本题解析:
本题难度:一般
4、选择题 小明沿直线上学,先以V1的平均速度走完前半位移,后以V2的平均速度走完后半位移,放学回家则前半时间以V1的平均速度,后半时间以V2的平均速度直线走回家,则小明上学和放学的平均速度大小分别是( )
A.
、
B.、
C.、
D.、
参考答案:设甲的平均速度v甲,乙的平均速度v乙,那么由.v=xt得
v甲=ssv1+sv2=2V1V2V1+V2
v乙=12V1t+12V2tt=V1+V22
故选:A.
本题解析:
本题难度:简单
5、选择题 一般变速直线运动的物体,加速度逐渐变小,直到为零,则物体的运动情况可能是( )
A.速度逐渐增大,加速度为零时速度最大
B.速度方向可能改变
C.速度逐渐减小,加速度为零时速度最小
D.速度逐渐增大,方向可能改变
参考答案:ABC
本题解析:
本题难度:简单