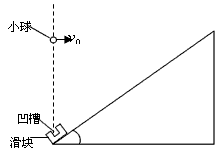
1、计算题  如图所示，倾角为37°的粗糙斜面的底端有一质量m=1kg的凹形小滑块，小滑块与斜面间的动摩擦因数μ=0.25。现小滑块以某一初速度v从斜面底端上滑，同时在斜面底端正上方有一小球以v0水平抛出，经过0.4s，小球恰好垂直斜面方向落入凹槽，此时，小滑块还在上滑过程中。（已知sin37°=0.6，cos37°=0.8，g=10m/s2），求：
（1）小球水平抛出的速度v0。
（2）小滑块的初速度v。
（3）0.4s内小滑块损失的机械能△E。

参考答案：解：（1）设小球落入凹槽时竖直速度为vy


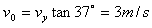
（2）小球落入凹槽时的水平位移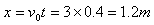
则滑块的位移为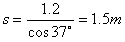

根据公式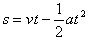
得：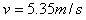
（3）
?

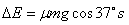
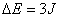
本题解析：

本题难度：困难

2、简答题  将一个物体以10m/s的速度从15m的高度水平抛出，求落地时她的速度大小和速度与地面的夹角？（不计空气阻力，取g=10m/s2）

参考答案：落地时在水平方向的分速度是
Vx=V0=10m/s?
竖直方向由匀变速运动规律知
Vy2-0=2gh?
由此得vy=

本题解析：

本题难度：一般

3、选择题  下列关于平抛运动的说法正确的是（　　）
A．平抛运动的竖直分速度不变
B．平抛运动的水平分速度逐渐增大
C．平抛运动的加速度不变
D．平抛运动的水平位移由初速度决定，与下落高度无关

参考答案：A、平抛运动在竖直方向上做自由落体运动，vy=gt随时间改变，故A错误；
B、平抛运动在水平方向上做匀速直线运动，水平速度不变，故B错误；
C、平抛运动只受重力，加速度为g，不变，故C正确；
D、平抛运动的水平位移x=v0t=v0

本题解析：

本题难度：一般

4、填空题  如图所示，是利用闪光照相研究平抛运动的示意图，小球由斜槽滚下，从桌边缘水平抛出，当它恰好离开桌边缘时，小球也同时下落，闪光频率为10 Hz的闪光器拍摄的照片中球有四个像，像间距离已在图中标出，单位为cm，两球恰在位置4相碰。

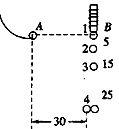
（1）计算球离开桌面时的速度__________。
（2）在图中画出球的运动轨迹并标明相对应的四个位置。

参考答案：（1）
（2）图“略”

本题解析：

本题难度：一般

5、简答题  一质量为m1=1kg、带电量为q=0.5c的小球/V静止在光滑水平平台上，另一质?量为m2=1kg、不带电的小球M自平台左端以速度v=4.5m/s向右运动，两小球发生完全?弹性碰撞后，小球N自平台右端水平飞出，碰撞过程小球N的电荷量不变，不计空气阻力，小球N飞离平台后由λ点沿切线落入竖直光滑圆轨道ABC，圆轨道ABC的形状为半径R＜4m的圆截去了左上角127°的圆弧，CB为其竖直直径，在过A点的竖直线00"的右边空间存?在竖直向下的匀强电场，电场强度大小为E=10V/m，（sin53°=0.8，cos53°=0.6，重力加速度g取?10m/s2）求：
（1）两球碰撞后小球N的速度大小vN
（2）小球N经过A点的速度大vA
（3）欲使小球N在圆轨道运动时不脱离圆轨道，求?半径R的取值应满足什么条件？

参考答案：（1）由题意，两小球发生完全弹性碰撞，根据动量守恒和机械能守恒，得
? m2v=m1vN+m2vM
? 12m2v2=12m1v2N+12m2v2M
联立解得：vN=4.5m/s
（2）小球离开平台后做平抛运动，由题知，小球经过A点时的速度沿圆轨道的切线方向，则
? cos53°=vNvA
解得vA=7.5m/s
（3）（i）小球N沿切线落入竖直光滑圆轨道ABC后，小球沿轨道做圆周运动，若恰好能通过最高点C，由重力和电场力的合力提供向心力，设滑至最高点的速度为vC，则有
? m1g+qE=m1v2CR
根据动能定理得：
-（m1g+qE）R（1+cos53°）=12m1v2C-12m1v2A
联立以上两式解得? R=2528m
故当0＜R≤2528m时，小球N沿着轨道做圆周运动的，且能从圆的最高点C飞出．
（ii）若小球N恰好滑到与圆心等高的圆弧上的T点时速度为零，则滑块也沿圆轨道运动而不脱离圆轨道．根据动能定理得
-（m1g+qE）Rcos53°=0-12m1v2A
解得，R=258m
根据题中信息可知R＜4m．故当258m≤R＜4m时，小球在轨道内来回的滚动．
综上所术，小球能沿圆轨道运动而不脱离圆轨道，半径R的取值应满足0＜R≤2528m或258m≤R＜4m．?
答：
（1）两球碰撞后小球N的速度大小vN是4.5m/s．
（2）小球N经过A点的速度大vA是7.5m/s
（3）欲使小球N在圆轨道运动时不脱离圆轨道，半径R的取值应满足0＜R≤2528m或258m≤R＜4m．

本题解析：

本题难度：一般