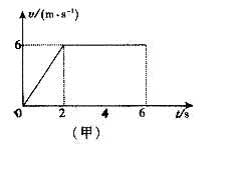
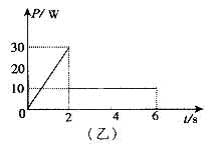
1、简答题  物体在水平地面上受水平力F的作用，在6s内速度v—t图线与F做功的功率P —t图线分别如图（甲）．（乙）所示。求物体与地面间的动摩擦因数为多少？
?

参考答案：0.15

本题解析：0.15（0~2s时，水平力F>f即F=f=ma；2~6s，物体做匀速运动，F′=f，由v—t图线和P—t图线可知0~2s，P="F·v=(f+ma)v" ①，?②，2s时，v=6m/s，代入①式，P=30W，2~6s，物体做匀速运动，?③，0~6s，整个过程中?④，解①②③④得μ=0.15。

本题难度：一般

2、计算题  随着33名被困地下长达69天的矿工安全获救，智利总统宣布将永久关闭圣何塞铜矿，充分体现了智利政府对生命的尊重。现假设竖直救生井的深度为700米，施救人员在井口自由释放小石块，经过多少时间可听到回音？（g取10m/s2，声速取340m/s，结果可以保留根号形式）

参考答案：

本题解析：略

本题难度：简单

3、选择题  一个做匀变速直线运动的质点，初速度为0.5m/s，第9s内的位移比第5s内的位移多4m，则该质点的加速度、9s末的速度和质点在9s内通过的位移分别是
A.a=1m/s2，v9=9m/s，x9=40.5m
B.a=1m/s2，v9=9m/s，x9=45m
C.a=1m/s2，v9=9.5m/s，x9=45m
D.a=0.8m/s2，v9=7.7m/s，x9=36.9m

参考答案：C

本题解析：分析：根据连续相等时间内的位移之差等于恒量求出加速度的大小，通过速度时间公式求出9s末的速度，通过位移时间公式求出9s内的位移．
解答：根据连续相等时间内的位移之差是一恒量知，，解得a=．
则9s末的速度v9=v0+at=0.5+1×9m/s=9.5m/s．
9s内的位移m=45m．故C正确，A、B、D错误．
故选C．
点评：解决本题的关键掌握匀变速直线运动的运动学公式和推论，并能灵活运用．

本题难度：简单

4、选择题  甲、乙两地在一条平直公路上，司机小李匀速开车，用100min可走过全程；而司机老张匀速开车，需用150min走完全程．现两人分别从甲、乙两地匀速对开，相遇时小李比老张多走了15km．则小李的车速为（　　）
A．0.6km/min
B．1.5km/min
C．1.0km/min
D．0.75km/min

参考答案：D

本题解析：

本题难度：简单

5、选择题  把一钢球系在一根弹性绳的一端，绳的另一端固定在天花板上，先把钢球托起（如图所示），然后放手．若弹性绳的伸长始终在弹性限度内，关于钢球的加速度a、速度v随时间t变化的图象，下列说法正确的是

A.甲为a-t图象
B.乙为a-t图象
C.丙为v-t图象
D.丁为v-t图象

参考答案：B

本题解析：分析：要注意进行全过程分析：由静止释放后由于绳子处于松弛状态小球的加速度a=g，速度v=gt；
绳子张紧后小球的加速度a==g-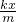，物体的加速度a逐渐减小，但速度逐渐增大；
当弹力等于重力时物体的加速度a=0，速度达到最大；
弹力大于重力时，加速度a=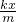-g，物体做加速度逐渐增大的变减速运动；
当物体的速度为0后物体开始向上做加速度逐渐减小的变加速运动，弹力等于重力后物体做加速度逐渐增大的变减速运动，当弹性绳恢复原长后速度向上，加速度a=g，即物体做竖直上抛运动．
解答：将小球由静止释放后由于绳子处于松弛状态，故小球仅受重力，故小球的加速度a=g，故a-t图象是一条水平的直线．
小球的速度v=gt，由于速度图象的斜率等于物体的加速度，故v-t图象是过坐标原点的一条直线．
绳子张紧后绳子的弹力F=kx，其中x为绳子的形变量
故小球的加速度a==g-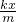，故随x的增大，物体的加速度a逐渐减小．但速度逐渐增大；故v-t图象的斜率逐渐减小．
当弹力等于重力时物体的加速度a=0，速度达到最大．
此后弹力大于重力，故小球所受合力方向竖直向上．加速度a=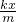-g，随x增大物体的加速度逐渐增大，方向竖直向上．由于速度方向向下，故物体做加速度逐渐增大的变减速运动．
当物体的速度为0后物体开始向上做加速度逐渐减小的变加速运动，此过程中速度方向向上，加速度方向也向上．当弹力等于重力后物体做加速度逐渐增大的变减速运动，它的速度方向向上，加速度方向方向向下．当弹性绳恢复原长后速度向上，加速度a=g，即物体做竖直上抛运动．
综上所述甲为v-t图象，乙为a-t图象．
故B正确．
故选B．
点评：解此类题目时不能急躁，要平心静气的进行详细的过程分析．

本题难度：困难